En 1937, quand Alfred Henry Sturtevant¹ pose cette question simple et pourtant extraordinairement importante : « Pourquoi le taux de mutation n’atteint-il jamais zéro ? » [1], la génétique, en particulier grâce à l’utilisation intensive des drosophiles comme modèle d’étude, a fait des progrès considérables depuis sa fondation quelques décennies auparavant. Quelques faits sont déjà bien établis : des individus mutants apparaissent de façon récurrente dans les populations, comme des mouches aux yeux blancs dans une population de mouches avec les yeux rouges ; ces individus mutants sont les descendants de parents porteurs de modifications (des mutations) dans des cellules de leur lignée germinale ; enfin, la plupart des mutations qui modifient le phénotype ont des effets délétères car ces mutants ont souvent une viabilité et/ou une fécondité réduite, voire nulle (si la mutation est létale ou rend le porteur stérile). Il est par ailleurs établi que le nombre de mutations qui se produisent par génération, ou taux de mutation, est variable dans les différentes lignées de drosophiles [2-4]. Le taux de mutation étant un caractère héréditaire et variable, il peut donc évoluer. Dans ce cadre, un taux de mutation réduit représente un avantage qui devrait conduire à la sélection des individus antimutateurs. En effet, les individus qui produisent le moins de descendants mutants produiront plus de descendants viables et fertiles à la génération suivante. Notons que la sélection ne se fait pas sur le phénotype de l’individu mutateur mais sur le phénotype de ses descendants, une forme de sélection appelée parfois sélection de second ordre. Progressivement, la sélection récurrente des individus les moins mutateurs, qui apparaissent au cours du temps, devrait faire tendre le taux de mutation vers zéro. Comme l’existence des mutations, à l’origine de la diversité génétique, est la condition sine qua non de l’évolution des espèces, l’évolution devrait donc, en théorie, s’arrêter faute de matière première ; or ce n’est manifestement pas le cas. Sturtevant en conclut que la nature des gènes, inconnue en 1937, « ne permet pas une telle réduction » et que « les mutations sont des accidents et que les accidents finissent toujours par survenir » [1]. Pour mieux comprendre le contrôle du flux de mutations et son évolution au cours du temps, il faudra attendre le dernier tiers du XX^e siècle. En effet, jusque-là, les mutations n’étaient qu’indirectement observables par le biais de leurs effets phénotypiques associés : modifications de couleur, de forme, de viabilité, de fertilité. Les mutations n’étaient donc définies, au mieux, que par une association entre une position sur un chromosome et un phénotype. Avec la découverte de méthodes de séquençage de l’ADN, il devient possible d’observer des différences entre génomes indépendamment de tout effet observable sur les organismes. L’accroissement récent des capacités de séquençage rend possible la quantification des différences à l’échelle des génomes entiers. Toutefois, si les mutations à petite échelle, comme le remplacement d’un nucléotide par un autre, une insertion ou une délétion de quelques nucléotides, sont facilement identifiables, les remaniements à grande échelle restent difficiles à étudier. C’est pour cela que les analyses du taux de mutation et de son évolution sont aujourd’hui essentiellement fondées sur l’identification de mutations ponctuelles (changement d’un nucléotide en un autre ou polymorphisme nucléotidique – SNP en anglais). Dans la suite de cet article, nous utiliserons le mot mutation dans le sens étroit de mutation ponctuelle car la plupart des travaux sont focalisés sur ce type de mutations, mais cela ne devrait pas modifier significativement la validité et la portée générale des mécanismes évolutifs mis en évidence.

Le nombre de mutations qui se produisent par unité de temps dépend en particulier des complexes protéiques impliqués dans la réplication et la réparation de l’ADN. Des mutations peuvent se produire dans les gènes qui codent ces protéines, il peut donc exister une variabilité génétique interindividuelle des mécanismes de réplication et de réparation de l’ADN, c’est-à-dire une variation interindividuelle du taux de mutation. Dans les cas les plus extrêmes, des mutations dans les gènes de réparation de l’ADN sont responsables de maladies génétiques extrêmement graves, comme le xeroderma pigmentosum ². Ces mutations ne sont pas maintenues au cours des générations car leurs porteurs ont une espérance de vie et des capacités de reproduction réduites. En théorie, à l’échelle de l’évolution, seules des mutations de ces gènes avec des effets plus réduits sur le taux de mutation des autres gènes devraient se maintenir dans les populations, mais nous verrons plus loin qu’il peut exister des exceptions à cette règle.

Les taux de mutation mesurés chez des organismes aussi divers que des virus à ARN, des virus à ADN, des bactéries, des eucaryotes unicellulaires et pluricellulaires sont relativement bas, mais ne sont jamais égaux à zéro et varient dans une gamme extrêmement étendue : de 10^-3 à 10^-11 mutations par site par réplication [5-7]. En d’autres termes, la probabilité qu’un nucléotide soit remplacé par un autre peut être proche de 1 sur mille chez des virus à ARN [7], mais être proche de 1 sur cent milliards chez des paramécies [8]. Chez l’homme, le taux de mutation par génération est d’environ 10^-8, soit moins de 10^-10 par réplication [9].

Les mutations qui n’ont pas d’effets sur le nombre de descendants sont invisibles du point de vue de la sélection naturelle : ce sont des mutations neutres. Les effets des mutations ponctuelles ont été caractérisés à de multiples reprises chez des organismes aussi différents que des virus et l’homme, en passant par des bactéries et des levures [10]. Toutes ces analyses montrent que la plupart des mutations qui apparaissent sont neutres, qu’une petite fraction est délétère et que les mutations avantageuses sont extrêmement rares. Très récemment, cette observation classique a pu être analysée très finement grâce à une technologie très sophistiquée qui permet l’analyse d’un très grand nombre de mutants chez la bactérie Escherichia coli [11]. Les mutations qui modifient le phénotype ont un effet le plus souvent légèrement délétère, beaucoup moins souvent franchement délétère, rarement létal et quasi jamais avantageux. Cette observation, qui peut paraître contre-intuitive, se comprend facilement si l’on considère que les systèmes génétiques sont les résultats de processus d’optimisation qui se sont déroulés pendant des millions, voire parfois des milliards d’années, et qu’il est donc aujourd’hui beaucoup plus facile de les détériorer que de les améliorer [12] (→).

(→) Voir le Forum de D. Casane et P. Laurenti, m/s n° 12, décembre 2014, page 1177

En 1967, Motoo Kimura, un des principaux théoriciens de la biologie évolutive, suggère qu’il doit y avoir une forte sélection contre les mutations qui augmentent le taux de mutation. Par ailleurs, il doit aussi exister une sélection contre un taux de mutation trop bas, car dans un environnement à long terme instable, il est nécessaire qu’il existe une diversité génétique (polymorphisme génétique) pour que l’adaptation puisse se réaliser. Sans ce polymorphisme, l’extinction devient inévitable. La baisse du taux de mutation à petite échelle évolutive impliquerait une sélection interindividuelle (intragroupe), alors que son maintien serait favorisé à long terme par une sélection intergroupe (entre populations ou espèces), de façon analogue aux mécanismes qu’on suppose à l’œuvre pour le maintien de la reproduction sexuée qui présente aussi un désavantage à court terme à l’échelle des individus, mais un avantage à long terme à l’échelle des populations [12]. Le taux de mutation observé correspondrait à un état d’équilibre entre deux forces de sélection qui agissent à des niveaux d’organisation différents. Le point d’équilibre dépend de l’environnement dans lequel vit une espèce. Si cet environnement est très stable, la pression pour maintenir de la variabilité sera faible et le taux de mutation tendra vers une valeur très basse sous l’effet de la sélection interindividuelle, alors que pour une espèce vivant dans un environnement très instable, un taux de mutation élevé sera maintenu. Si Kimura ne doute pas de l’existence de la sélection contre les allèles mutateurs qui augmente le taux de mutation des génomes, il doute fortement de l’existence d’une sélection contre les allèles antimutateurs qui mène vers un taux de mutation trop bas. Il propose donc une autre explication aux taux de mutation observés : ils correspondent aux taux de mutation les plus bas possibles, en tenant compte du fait qu’il y a peut-être une limite biochimique à l’amélioration des systèmes de réplication et de réparation qui ne peut être franchie. On peut aussi supposer un coût, en terme énergétique par exemple, de la réduction du taux de mutation et que ce coût peut devenir trop important pour pouvoir être supporté par un organisme. Au début des années 1970, il n’était pas possible de tester toutes ces hypothèses.

Depuis une dizaine d’années, Michael Lynch^3, propose de tenir compte d’un paramètre négligé jusqu’alors : la taille finie des populations d’organismes vivants. En effet, les fréquences des allèles varient au cours du temps du fait de leur valeur sélective, mais aussi du seul fait du hasard de l’échantillonnage des gamètes à l’origine des individus qui constituent une nouvelle génération. Par exemple, un allèle peut être présent avec une fréquence de 0,5 à une génération donnée, puis être présent à une fréquence de 0,6 à la génération suivante, du seul fait de ce processus d’échantillonnage. Cette variation aléatoire des fréquences, qu’on appelle la dérive génétique, sera d’autant plus grande que la population est de petite taille. Dans une très petite population, un allèle peut ainsi se fixer ou disparaître en quelques générations sans qu’il ait un effet sur la fitness⁴. Dans les grandes populations, ces fluctuations stochastiques sont de faibles amplitudes et le polymorphisme génétique peut se maintenir pendant un grand nombre de générations. Les généticiens s’intéressent ainsi à ce qu’ils appellent l’effectif efficace de la population (N_e) plutôt qu’au nombre d’individus qui la constituent. N_e peut être considéré, en première approximation, comme le nombre d’individus qui se reproduisent à chaque génération. L’effectif efficace est donc souvent beaucoup plus petit que l’effectif réel d’individus. Une forte variance du nombre de descendants parmi les individus qui se reproduisent et de fortes fluctuations de la taille de la population au cours du temps réduisent aussi beaucoup la valeur de N_e. Pour fixer les idées, on estime à 10 000 l’ordre de grandeur de l’effectif efficace à long terme de l’espèce humaine dans son ensemble. L’effectif efficace est un paramètre difficile à estimer, et on utilise souvent le polymorphisme génétique neutre pour l’évaluer. En effet, les grandes variations de fréquences alléliques dans les petites populations conduisent à une élimination plus rapide du polymorphisme. En conséquence, s’il y a peu de polymorphisme, on estimera que N_e est petit. À l’inverse, s’il y a beaucoup de polymorphisme, on estimera N_e grand. Pour un allèle soumis à sélection, s’il y a peu de dérive génétique (N_e grand), il se fixera (sa fréquence atteindra 1) presque sûrement s’il est avantageux, et il sera presque sûrement éliminé s’il est délétère. Mais ce même allèle peut se fixer alors qu’il est délétère ou être perdu alors qu’il est avantageux, s’il y a de fortes fluctuations stochastiques des fréquences alléliques (N_e petit) qui perturbent les effets de la sélection directionnelle.

En résumé, les effets de la sélection naturelle peuvent être réduits à néant par la dérive génétique d’autant plus que cette dernière est forte et que l’avantage (ou désavantage) sélectif est faible (pour une explication plus détaillée voir [13], et une analogie footballistique présentée dans l’Encadré « le football évolutionnaire »). La dérive génétique est donc une barrière à la sélection naturelle quand cette dernière est de faible ampleur. Lynch propose que c’est cette barrière qui s’oppose à la réduction continue vers zéro du taux de mutation et il rejette l’hypothèse que le taux de mutation soit le résultat de la sélection pour une valeur optimale. Il propose également que les espèces qui ont le taux de mutation le plus faible sont celles qui ont les effectifs efficaces les plus grands et donc chez lesquelles la sélection pour un taux de mutation bas est la plus efficace [14].

Nous allons maintenant examiner un ensemble de résultats récents et très divers qui permettent de tester quelques hypothèses et des attendus associés à ces différents modèles pour expliquer l’existence des mutations et l’extrême variabilité de leur fréquence d’apparition chez différents organismes

Question à laquelle il est très difficile de répondre pour les organismes multicellulaires, mais qui est plus facilement testable chez des organismes unicellulaires en faisant des expériences de mutagenèse pour générer des allèles antimutateurs qui réduisent le taux de mutation. C’est ainsi qu’il est possible d’abaisser le taux de mutation chez la bactérie E. coli pourtant à l’origine déjà très bas (~10^-10) [15, 16]. Bien qu’il soit souhaitable de tester d’autres espèces, ce résultat suggère néanmoins que le taux de mutation observé dans les populations naturelles n’est pas le plus bas possible.

Question à nouveau difficile à aborder expérimentalement, mais qui a pu être testée chez un virus à ARN [17]. Les virus à ARN sont connus pour avoir un taux de mutation extrêmement élevé, mais ce n’est pas toujours le cas [17]. Dans le cadre du modèle d’équilibre entre le fardeau de mutations (les nouvelles mutations délétères à éliminer) et la nécessité de générer des mutations adaptatives, un taux de mutation élevé est supposé être la conséquence d’un besoin d’adaptation fréquent [18]. Ainsi, le taux très élevé de mutation d’un virus comme le VIH (virus de l’immunodéficience humaine), le menant à la limite du fardeau de mutation supportable, serait nécessaire à son adaptation rapide et récurrente au système immunitaire de son hôte et aux traitements médicaux [17]. L’équipe de Furio et al. [17] montre que l’augmentation de la fidélité de la réplication par mutation de l’ARN polymérase se fait au prix d’un ralentissement du taux de réplication, induisant une réduction de la valeur sélective. Les lignées les plus mutatrices ne présentent pas une meilleure adaptabilité. Les auteurs en concluent que le taux de mutation est un équilibre résultant de deux forces sélectives opposées, le fardeau de mutations favorisant les taux de mutation faibles et la vitesse de réplication favorisant les taux de mutation élevés.

Des taux de mutation très élevés ne sont observés que chez certains virus, mais jamais chez les procaryotes, ni chez les eucaryotes. On peut faire l’hypothèse que ces virus vivent dans des environnements beaucoup plus instables que les autres virus et les organismes cellulaires. Non seulement c’est assez peu convaincant, mais une autre explication est suggérée par l’observation d’une corrélation négative entre la taille du génome et le taux de mutation [5]. Cette corrélation est encore plus évidente en considérant la taille efficace du génome. La taille efficace du génome est la partie du génome soumise à sélection, c’est-à-dire la part du génome où les mutations ne sont pas neutres ; soit pratiquement la totalité du génome chez la plupart des virus et des procaryotes, mais souvent seulement une petite partie du génome des eucaryotes qui est composé essentiellement de séquences intergéniques. La taille efficace d’un génome est souvent estimée, en première approximation, en additionnant la longueur des séquences codant les protéines. Il est attendu que plus un génome contient de séquences codantes, plus le nombre de sites soumis à sélection est important, c’est-à-dire plus de sites qui, s’ils mutent, auront un effet négatif sur la valeur sélective. Focalisons-nous maintenant sur les mutations létales pour faire un petit calcul simple. 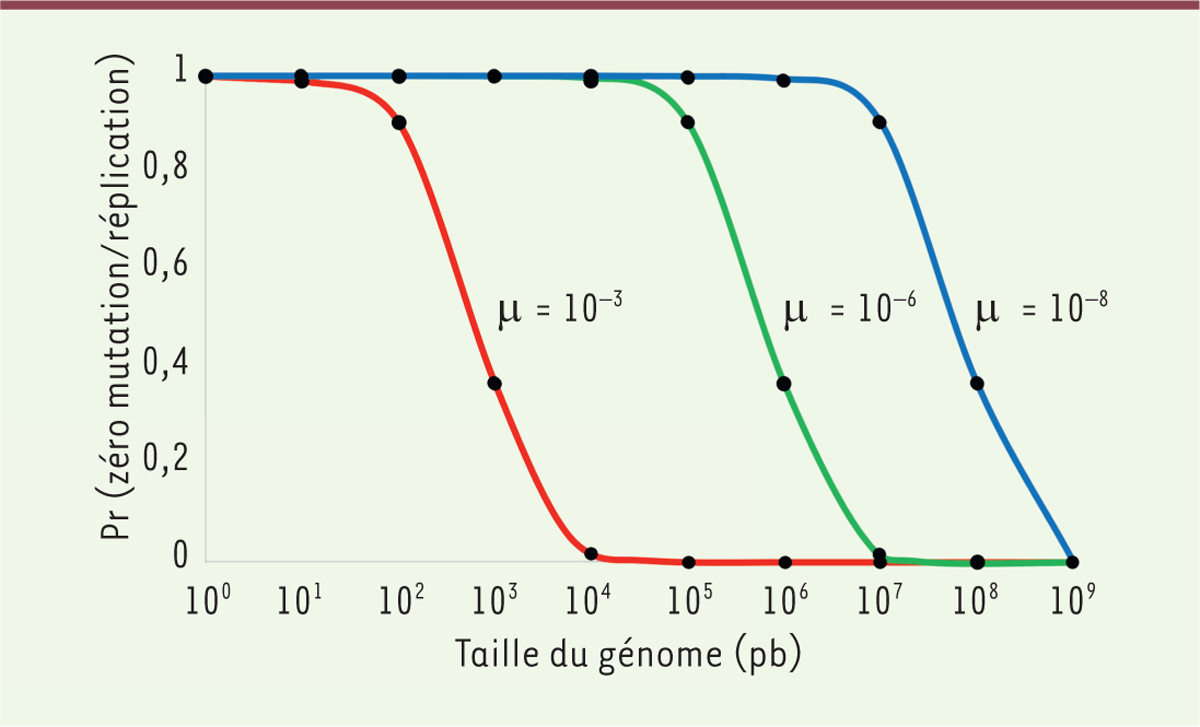Si un génome contient 1 000 nucléotides invariables, qui ne peuvent être mutés sans conséquence létale pour le porteur, alors la probabilité de répliquer ce génome sans qu’il y ait une seule mutation à ces mille positions est égal à (1-m)^1 000 (m étant le taux de mutation). Cette probabilité peut être calculée en fonction du nombre de sites invariables et pour différents taux de mutation (Figure 1). Pour un taux de mutation égal à 10^-3, un génome contenant moins de mille sites invariables (soit seulement quelques gènes) peut produire des copies sans mutation, donc fonctionnelles. Pour ce même taux de mutation, un génome contenant plus de 10 000 sites invariables ne pourra pas produire de copies fonctionnelles. Ainsi, un virus ne contenant que quelques gènes peut avoir un fort taux de mutation sans que cela empêche la production de copies fonctionnelles du génome. Les procaryotes et les eucaryotes contiennent entre quelques centaines et quelques dizaines de milliers de gènes, ce qui implique nécessairement bien plus de 10 000 sites invariables et donc l’impossibilité d’observer un tel taux de mutation. Par exemple, le génome humain contient un peu plus de 20 000 gènes dont la longueur moyenne de la partie codante est d’un peu plus de 1 000 paires de bases, soit au total plus de 20 millions de nucléotides constituant les séquences codant les protéines. Sans même considérer les séquences non-codantes ultra-conservées qui sont aussi soumises à la sélection, et en tenant compte que seule une fraction des séquences codantes ne peut pas être modifiée sans conséquence létale, il existe plusieurs millions de positions invariables parmi les 3,2 milliards de nucléotides par génome haploïde. Dans une telle situation, seul un taux de mutation inférieur à 10^-8 permet de produire une forte proportion de génomes fonctionnels (Figure 1). Le taux de mutation maximal étant limité par la taille efficace du génome, on peut en déduire qu’au cours de l’évolution, l’augmentation de la taille efficace d’un génome ne peut se faire qu’en association avec la réduction du taux de mutation. S’il s’avérait qu’il est très difficile d’améliorer les taux de mutation les plus bas observés, alors ceci pourrait expliquer que le nombre de gènes dans des génomes plafonne toujours à quelques dizaines de milliers.

Figure 1. Probabilité d’une réplication sans mutation en fonction de la taille du génome et du taux de mutation. μ : taux de mutation ; pb : paire de bases ; Pr : probabilité.

Figure 1. Probabilité d’une réplication sans mutation en fonction de la taille du génome et du taux de mutation. μ : taux de mutation ; pb : paire de bases ; Pr : probabilité.

Les analyses théoriques décrites précédemment convergent pour nous amener à conclure que chez des organismes dont le génome est constitué de plusieurs milliers de gènes et dans un environnement relativement stable, le taux de mutation doit tendre vers zéro mais rester au-dessus d’une limite imposée par les propriétés physico-chimiques des complexes moléculaires qui répliquent et réparent l’ADN et par la nécessité de produire des mutations à valeur adaptative. Lynch a proposé que s’il ne tend pas vers zéro, c’est plutôt parce que la sélection pour des taux de mutation toujours plus bas devient de plus en plus difficile car les différences de valeurs sélectives deviennent de plus en plus faibles. Pour comprendre ce point, imaginons un taux de mutation de 10^-1 dans une population dans laquelle apparaît un individu avec un taux de mutation dix fois plus faible, soit 10^-2. La différence des nombres de descendants viables produits par ce mutant par rapport aux autres individus sera importante. Mais si le taux de mutation est de 10^-8 dans une population dans laquelle apparaît un individu avec un taux de mutation dix fois plus faible, soit 10^-9, cette différence sera très faible car dans cette population, la plupart des descendants sont viables. En d’autres termes, plus un système est optimisé, plus son amélioration par le mécanisme de sélection de nouveaux allèles devient difficile dans une population de taille finie, car son action est de plus en plus faible et donc d’autant plus perturbée par la dérive génétique qui augmente ou réduit de façon aléatoire la fréquence des allèles antimutateurs. Dans une population de taille efficace très grande, la dérive génétique étant plus faible, la sélection devrait amener le taux de mutation vers des valeurs plus petites (Figure 2). 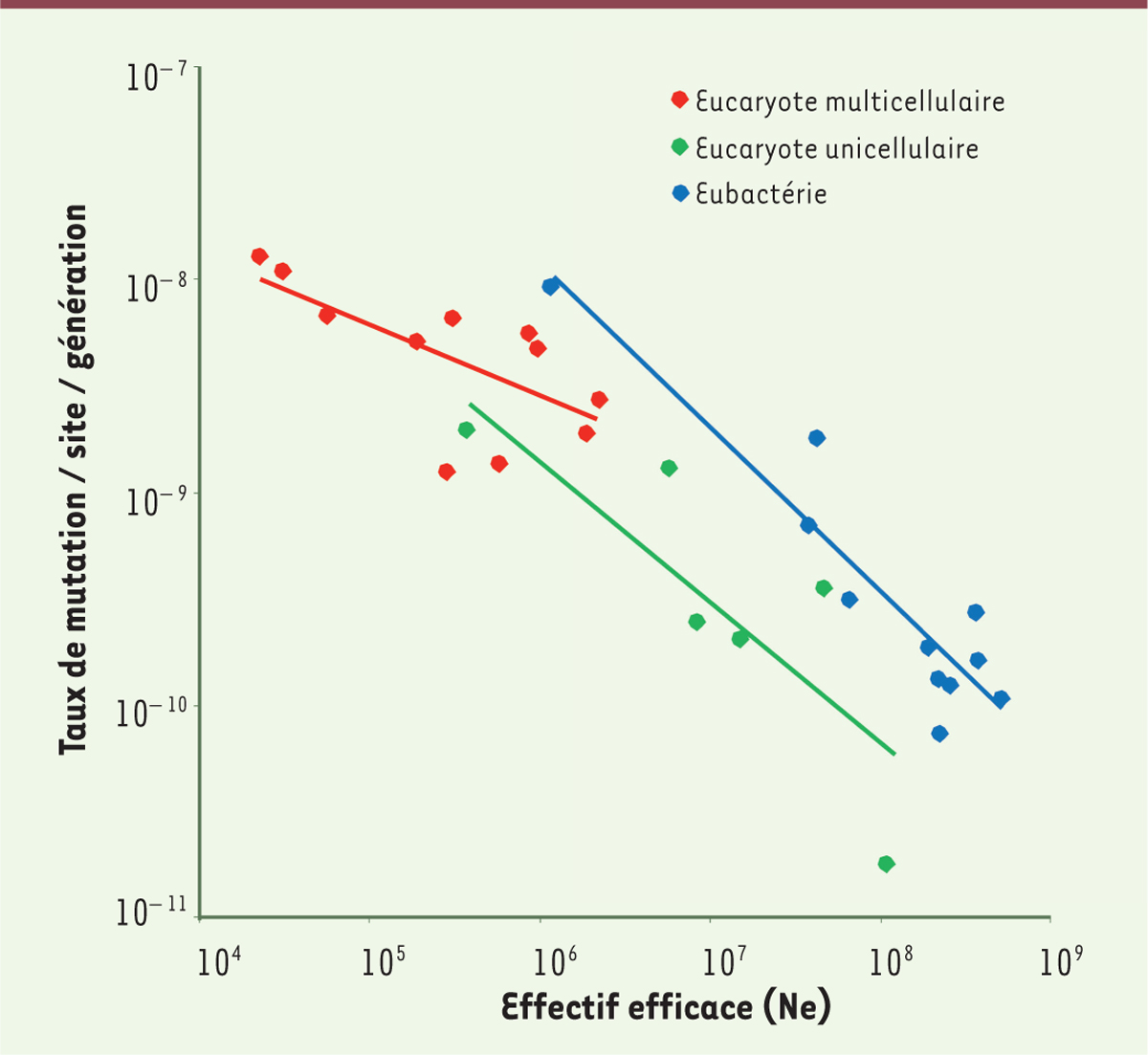Cet attendu est largement vérifié, aussi bien pour les mutations ponctuelles [9, 14, 19] que pour le taux d’insertion/délétion de courtes séquences [20]. Ainsi, le taux de mutation est corrélé négativement à la taille efficace des populations (Figure 3) : les bactéries ont des tailles efficaces souvent plus grandes que celles des eucaryotes et des taux de mutation plus faibles ; les eucaryotes unicellulaires ont des tailles efficaces souvent plus grandes que celles des pluricellulaires et des taux de mutation plus faibles.

Nous avons discuté des contraintes agissant sur l’évolution du taux de mutation, en particulier la sélection naturelle qui favorise les individus antimutateurs au travers d’une meilleure valeur adaptative de leurs descendants. C’est donc le taux de mutation dans la lignée germinale qui est importante ici. Même si beaucoup de mutations se produisent dans les lignées somatiques, c’est finalement peu important car ces mutations disparaîtront toutes à la mort de l’individu. On peut donc supposer que les lignées somatiques sont soumises à une sélection moins forte pour réduire le taux de mutation, et c’est effectivement ce qui est observé [9].

Nous venons de décrire des arguments théoriques et expérimentaux qui suggèrent que le taux de mutation dans une espèce donnée dépend principalement de 1) la taille efficace de son génome qui définit le taux de mutation maximum et 2) l’effectif efficace qui contrôle le taux de mutation minimum accessible, c’est-à-dire au-dessus de la barrière de la dérive génétique. Il est attendu que le taux de mutation pourra donc fluctuer autour du taux de mutation minimum accessible au gré des allèles mutateurs et antimutateurs qui apparaîtront au cours du temps.

Nous pouvons introduire maintenant un niveau de complexité supplémentaire en tenant compte du fait que des espèces possèdent une reproduction sexuée (la plupart des eucaryotes) et d’autres non (les procaryotes). Nous allons voir que cette différence a des conséquences sur l’évolvabilité du taux de mutation. Chez les procaryotes, si une cellule a un fort taux de mutation alors, dans des conditions où une mutation est nécessaire pour s’adapter à l’environnement, il est probable que cette mutation utile apparaisse chez un descendant de la cellule mutatrice. Sans reproduction sexuée, il y a peu de recombinaisons des génomes et l’allèle muté se fixera dans la population en association avec l’allèle mutateur (c’est l’effet auto-stop, Figure 4. En parallèle de son adaptation, la population aura acquis un fort taux de mutation. Si une cellule, tout en gardant l’allèle utile, perd l’allèle mutateur, elle sera avantagée car elle restera adaptée à l’environnement et elle réduira le fardeau de mutation dû à l’allèle mutateur. Ainsi, dans des milieux instables, il peut se mettre en place des cycles dans lesquels des populations de bactéries voient leur taux de mutation augmenter fortement puis revenir vers des valeurs beaucoup plus basses. Bien décrit sur le plan théorique, ce processus a été observé aussi bien dans des population expérimentales que naturelles de bactéries E. coli [21-27]. Chez une espèce à reproduction sexuée, si une mutation utile apparaît associée à un allèle mutateur, la recombinaison sépare rapidement les deux allèles, il n’y a pas d’effet auto-stop et il est donc peu probable de pouvoir identifier des populations mutatrices apparues par ce mécanisme [28] (Figure 4).

Figure 2. Effets de la sélection et de la dérive génétique sur le taux de mutation. A, B. sans dérive génétique, le taux de mutation est un équilibre entre des forces sélectives opposées favorisant les organismes mutateurs et antimutateurs. C, D. la dérive génétique pousse l’équilibre vers des valeurs plus grandes que celles attendues du seul fait de la sélection. Ne : effectif efficace de la population.

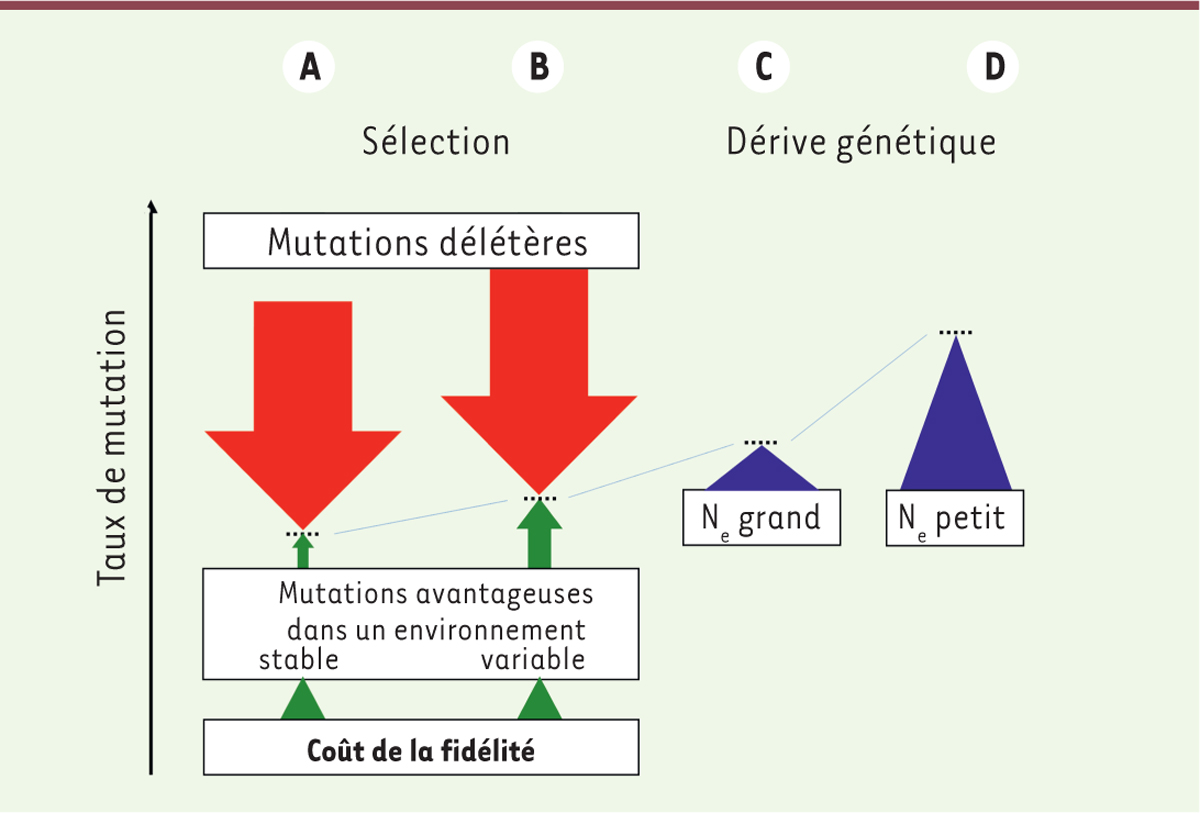
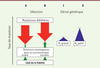Figure 2. Effets de la sélection et de la dérive génétique sur le taux de mutation. A, B. sans dérive génétique, le taux de mutation est un équilibre entre des forces sélectives opposées favorisant les organismes mutateurs et antimutateurs. C, D. la dérive génétique pousse l’équilibre vers des valeurs plus grandes que celles attendues du seul fait de la sélection. Ne : effectif efficace de la population.

Figure 3. Corrélation entre le taux de mutation et l’effectif efficace (modifié d’après Lynch et al. [14]).

Figure 3. Corrélation entre le taux de mutation et l’effectif efficace (modifié d’après Lynch et al. [14]).

Figure 4. Effet du mode de reproduction sur le taux de mutation. A. Dans une population à reproduction clonale, du fait de la liaison totale des gènes, par effet auto-stop, l’allèle « mutateur » se fixe dans la population avec l’allèle favorable. L’élimination de l’allèle mutateur implique une réversion ou le transfert horizontal d’un allèle non-mutateur. B. Dans une population à reproduction sexuée, la recombinaison dissocie rapidement l’allèle mutateur de l’allèle favorable si la liaison n’est pas très forte, diminuant ainsi l’effet auto-stop et la probabilité de fixation de l’allèle mutateur en même temps que l’allèle favorable (modifié d’après Sniegowski et al. [5]).

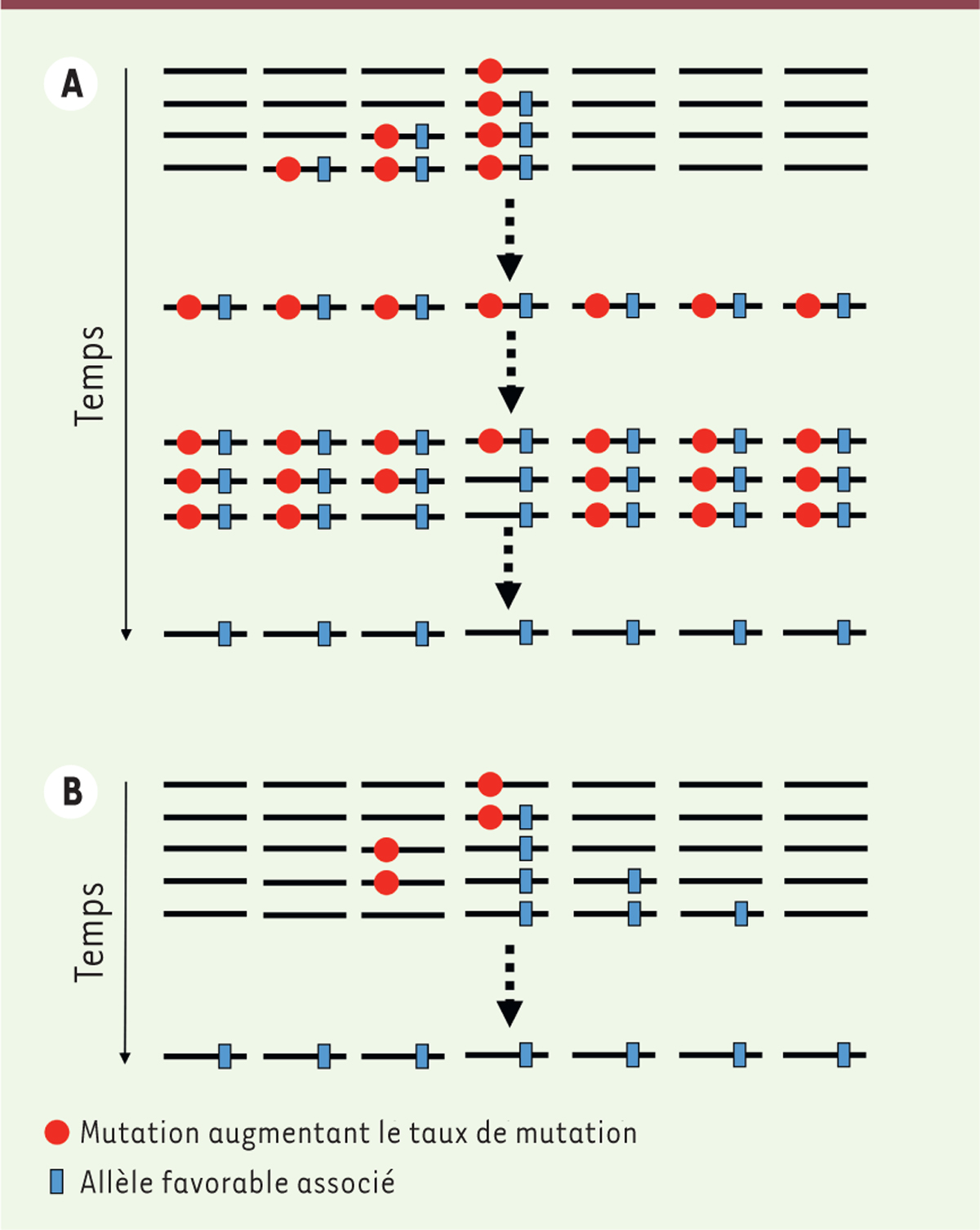
Figure 4. Effet du mode de reproduction sur le taux de mutation. A. Dans une population à reproduction clonale, du fait de la liaison totale des gènes, par effet auto-stop, l’allèle « mutateur » se fixe dans la population avec l’allèle favorable. L’élimination de l’allèle mutateur implique une réversion ou le transfert horizontal d’un allèle non-mutateur. B. Dans une population à reproduction sexuée, la recombinaison dissocie rapidement l’allèle mutateur de l’allèle favorable si la liaison n’est pas très forte, diminuant ainsi l’effet auto-stop et la probabilité de fixation de l’allèle mutateur en même temps que l’allèle favorable (modifié d’après Sniegowski et al. [5]).

La question « Pourquoi le taux de mutation n’est-il jamais égal à zéro » pourrait sembler triviale au premier abord : s’il n’y avait pas de mutations, il n’y aurait pas eu d’évolution et puisqu’il y a évolution, il y a donc bien eu des mutations, fermez le ban ! Elle a pourtant été à l’origine d’une suite de réflexions théoriques et de travaux expérimentaux d’une grande subtilité. Il reste beaucoup de questions ouvertes concernant ce point très important de la biologie évolutive, mais le voile se lève peu à peu. L’ensemble des approches disponibles aujourd’hui montre que la production de mutations, matériel de base de l’évolution, est elle-même un processus soumis aux mécanismes évolutifs qui dépendent de façon complexe de l’architecture des génomes des différentes espèces ainsi que de la stabilité des environnements dans lesquels elles vivent, et de leur démographie.

Les auteurs déclarent n’avoir aucun lien d’intérêt concernant les données publiées dans cet article.

Nous remercions chaleureusement nos collègues Jean-Luc Da Lage et Julien Fumey pour leurs fort pertinents commentaires et suggestions au cours de l’élaboration de cet article.