On tient désormais pour certain que la maîtrise des habiletés en numératie et en littéracie influence sensiblement les chances de réussite dans la vie de celui qui les possède (OCDE, 2013). Les travaux scientifiques traitant de ces dimensions chez les personnes avec une déficience intellectuelle (DI) restent néanmoins peu abondants (Browder et coll., 2012). Cet état de fait s’explique en partie par le déficit de reconnaissance du handicap qui caractérise les politiques nationales (ONFRIH, 2011) et internationales (OST, 2008) en matière de recherche.

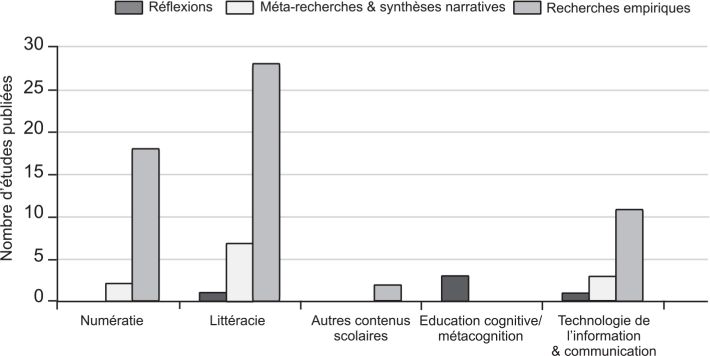
En ce qui concerne les travaux scientifiques s’intéressant aux savoirs scolaires chez les personnes avec une déficience intellectuelle, les études portant sur la littéracie sont plus nombreuses que celles traitant de la numératie. Ce déséquilibre, illustré dans la figure 11.1, est observé bien que ces deux champs de compétences soient massivement sollicités dans la vie quotidienne (domicile, travail, loisirs, etc.). En dehors de la littéracie et de la numératie, l’apprentissage des autres matières scolaires chez les personnes avec une DI reste quasiment inexploré actuellement (figure 11.1).

Ce chapitre abordera plus en détail la numératie, la littéracie sera quant à elle abordée dans la communication intitulée « Littéracie et déficience intellectuelle » de B-M. Martini-Willemin, dans la partie II de cet ouvrage. La numératie renvoie à une gamme d’habiletés très diverses qui implique le traitement et la manipulation des nombres et des contenus mathématiques.

Plus précisément, elle est définie comme « la capacité de localiser, d’utiliser, d’interpréter et de communiquer de l’information et des concepts mathématiques afin de s’engager et de gérer les demandes mathématiques de tout un éventail de situations de la vie (…). À cette fin, la numératie implique la gestion d’une situation ou la résolution d’un problème dans un contexte réel, en répondant à un contenu/à des informations/à des concepts mathématiques représentés de différentes manières » (OCDE, 2013, p. 63).

Les diverses facettes de la numératie énumérées ci-dessus sont étudiées avec une intensité variable dans la littérature spécialisée consacrée aux personnes avec une DI. Abstraction faite du public, les études se sont principalement intéressées aux habiletés et connaissances mathématiques précoces parfois de façon dispersée (Wilson et Räsänen, 2009), ainsi qu’aux habiletés classiquement acquises durant la période préscolaire et primaire (Bull, 2007 ; Foegen, 2008). Les habiletés sous-tendant les opérations plus complexes (algèbre, etc.), de même que la résolution de problème ont, par contre, été beaucoup moins étudiées (Kroesbergen et Van Luit, 2003 ; Inserm, 2007 ; Faragher et Clarke, 2014). Ce décalage est encore plus marqué dans les études concernant les personnes avec une déficience intellectuelle (Murphy et Mazzocco, 2008).

Parmi les thématiques les plus étudiées figurent :

• les connaissances et capacités de quantification, c’est-à-dire de représentation de la numérosité. Ces habiletés s’organisent autour de trois procédures complémentaires mais distinctes à savoir, les procédures consistant à subitizer (capacité à appréhender d’un coup d’œil une petite quantité quelle que soit la configuration des éléments), à estimer (globalement) et à compter de façon exacte ;

• les capacités lexicales numériques. Ces habiletés renvoient à la capacité de se référer aux étiquettes des nombres, ainsi qu’à la capacité de les manipuler et de les transposer d’un format symbolique à un autre (par exemple, transcoder du code arabe au code verbal écrit : 11 versus onze) ;

• les opérations arithmétiques simples (addition, soustraction, etc.) avec ou sans calculette ;

• les habiletés numériques fonctionnelles. Ces habiletés renvoient à la capacité de comprendre et d’utiliser les informations numériques dans diverses situations de la vie réelle. Dans ce domaine, l’utilisation et la gestion pratique de l’argent par les personnes avec une DI ont été particulièrement étudiées (Xin et coll., 2005 ; Faragher et Clarke, 2014).

Les habiletés numériques sont une composante forte à l’adaptation. Elles sont sollicitées dans une large gamme de tâches pratiques qu’elles ne manquent pas d’impacter en cas de déficit. Des compétences comme dénombrer une collection d’objets, payer, rendre la monnaie, faire un budget, comparer des prix, gérer des quantités, respecter la dose prescrite lors de la prise de médicaments jouent un rôle crucial pour répondre aux exigences du quotidien (Xin et coll., 2005).

Des compétences comme lire l’heure, comprendre un horaire, choisir le bon numéro de bus ou la bonne chaîne de TV, estimer ou comparer des durées, des quantités, des longueurs, mesurer, calculer, comprendre et interpréter des informations numériques sont également intensément sollicitées dans la vie de tous les jours.

Comme pour toute autre personne, la maîtrise de la numératie est cruciale pour la qualité de vie des personnes avec une DI. L’analyse réalisée par Faragher et Brown (2005) chez cinq adultes avec une trisomie 21, âgés entre 22 et 38 ans, montre que ces compétences sont requises dans la plupart de leurs contextes de vie. La maîtrise des compétences numériques conditionne l’indépendance de ces individus et représente « une question de qualité de vie » (Faragher et Brown, 2005).

La place capitale qu’occupe la numératie dans la vie quotidienne – privée et professionnelle – justifie que chaque pays mette en œuvre des politiques qui « associent une formation initiale de qualité à des opportunités et des mesures d’incitation qui invitent l’ensemble de la population à continuer à développer ses compétences en compréhension de l’écrit et en numératie, dans le cadre privé ou professionnel, une fois la formation initiale achevée » (OCDE, 2013, p. 13).

Actuellement, les habiletés en numératie ont surtout été étudiées chez les personnes porteuses d’une DI de nature syndromique (syndrome de Williams, trisomie 21, syndrome velo-cardio-facial, syndrome de l’X fragile ou d’alcoolisme fœtal ; cf. Hodapp et coll., 2003 ; Hodapp et Dykens, 2004). La recherche s’est peu intéressée aux habiletés numériques des personnes ayant une DI idiopathique1 . Or, ces personnes ne sont pas épargnées par les difficultés en numératie et/ou en littéracie (Carrasumada et coll., 2006). Des difficultés dans ces domaines constituent parfois les premiers signes de l’existence de la DI. Comme le rappellent Glidden et Schoolcraft (2007) : « parce que la déficience intellectuelle peut ne pas avoir d’étiologie médicale connue, son diagnostic est, en partie, basé sur les attentes de comportement dans la société. Dans une société dans laquelle les exigences de raisonnement abstrait ou celles de maîtrise de littéracie et numératie sont peu élevées, de nombreux individus avec une déficience intellectuelle légère peuvent ne pas être identifiés. En revanche, dans notre société, beaucoup d’enfants avec une déficience intellectuelle légère sont diagnostiqués non par le corps médical mais plutôt par les psychologues travaillant dans le contexte éducatif, car leurs difficultés scolaires sont susceptibles d’être la première indication formelle de l’existence d’un déficit intellectuel et du comportement adaptatif » (p. 393).

La recherche montre que certains désordres génétiques donnent lieu à des profils particuliers de compréhension de la numératie. Il est toutefois rare que la spécificité du phénotype cognitif soit totale et qu’un syndrome soit caractérisé par un ensemble de traits qui n’appartiennent qu’à lui seul. Plus généralement, le profil cognitif dégagé dans un syndrome a une spécificité partielle, c’est-à-dire qu’il peut également se retrouver dans d’autres syndromes (Dykens et coll., 2000).

Cependant, les comparaisons inter-syndromiques, qui mettent en évidence l’existence de profils de forces et de faiblesses distincts dans certains sous-groupes étiologiquement bien délimités, peuvent être utiles pour comprendre les difficultés rencontrées par les personnes avec une DI idiopathique. Les données issues des études syndromiques peuvent servir de modèles pour la compréhension des troubles dans d’autres conditions cliniques (Mazzocco, 2007).

Camp et coll. (2011) rappellent que le développement de la représentation du nombre doit être considéré dans ses relations avec les autres systèmes cognitifs. Les tâches numériques, mêmes les plus simples, font appel à plusieurs fonctions cognitives générales (Kroesbergen et Van Luit, 2003 ; Inserm, 2007 ; Passolunghi et Lanfranchi, 2012). Parmi les fonctions impliquées, citons :

• la mémoire de travail (MdeT) qui est reconnue comme une compétence clé pour le développement des habiletés mathématiques (Lemaire et coll., 1996 ; Meyer et coll., 2010 ; Passolunghi et Lanfranchi, 2012). Elle comprend notamment : la boucle phonologique, autrement dit la MdeT verbale, qui est mobilisée lors de la réalisation des calculs mentaux, lesquels supposent le maintien des nombres en mémoire. L’efficacité de la MdeT est elle-même tributaire de la vitesse de traitement (Barrouillet et coll., 2007 et 2009 ; Rose et coll., 2011) ; le calepin visuo-spatial (MdT visuo-spatiale) qui joue un rôle particulier dans la capacité d’appréhender les figures géométriques, les diagrammes ou les courbes. Il sous-tend aussi les capacités de rotation mentale (Jarvis et Gathercole, 2003 ; Kyttälä, 2008 ; Kyttälä et coll., 2003 ; Passolunghi et Cornoldi, 2008) et la capacité de manipuler la ligne numérique mentale (Zorzi et coll., 2002 et 2006) ; l’administrateur central qui assure la manipulation des informations aux différentes étapes de la tâche (ex. calcul mental, etc.) ;

• la mémoire à long terme (MLT) qui intervient notamment dans la récupération de faits mathématiques2 connus comme par exemple, les tables de multiplication ;

• les fonctions exécutives qui coordonnent le travail à réaliser dans les tâches numériques (Szücs et coll., 2014). Le fonctionnement exécutif est lui-même étroitement lié à la MdeT, à la vitesse de traitement et à l’attention, dans la mesure où il contribue et est à la fois dépendant du partage des ressources (Passolunghi et Lanfranchi, 2012 ; Camos et Barrouillet, 2013). Tout déficit perturbera, voire impactera, la réalisation des tâches devant être assurées solidairement par un ou plusieurs sous-systèmes cognitifs ;

• le langage, qui est en étroite relation avec le système de représentation symbolique des nombres (par exemple la chaîne numérique verbale, la maîtrise du vocabulaire et des signes mathématiques, par exemple « plus », « moins », « égal », etc.). Donlan (2009) a réalisé une très bonne synthèse sur le rôle du langage dans le développement des concepts mathématiques.

Le bon fonctionnement des processus cognitifs généraux facilite l’acquisition des habiletés mathématiques. À l’inverse, des déficits dans un ou plusieurs de ces systèmes peuvent avoir des conséquences sur l’acquisition et/ou la maîtrise des habiletés numériques (Riccio et coll., 2010). Le tableau 11.I synthétise les principaux retentissements d’un déficit des systèmes cognitifs généraux sur le traitement numérique.

Les observations issues des travaux menés en psychologie neurodéveloppementale, en neuropsychologie et en psychologie cognitive, s’accordent sur le fait que la représentation numérique serait sous-tendue par deux systèmes distincts : le système analogique de représentation des magnitudes (= ordre de grandeur) (voir Dehaene, 2011 pour une synthèse) et le système de représentation symbolique (voir Carey, 2009 pour une synthèse).

Le système de représentation « analogique » est activé lorsque les stimuli numériques à traiter se présentent sous une forme concrète, par exemple matérielle (collection d’objets réels) ou figurative (nombre d’éléments dans une figure). Selon le nombre d’éléments, le traitement est exact (N éléments <3) ou approximatif (N éléments >3). Ce système permet de capter la magnitude d’une collection ou d’un arrangement d’objets. Il a aussi comme fonction de comparer et de discriminer deux collections en fonction de leur numérosité. Le traitement exact n’est possible que lorsque la numérosité est inférieure à 3. Avec des collections plus importantes, le nombre d’éléments est estimé de façon approximative (Butterworth, 1999 et 2010). Le système analogique renvoie à ce qui est communément appelé le « sens [ou intuition fondamentale] des nombres » (Dehaene, 1997).

Le système de représentation « symbolique » traite les stimuli numériques présentés sous forme de signes conventionnels, graphiques (chiffres lus ou écrits : [3]) ou vocaux (informations numériques reçues ou émises verbalement : /trois/). Ce système de représentation, qui s’origine dans le développement symbolique et dans le langage, suppose des phases d’intégration successives (chaîne numérique verbale, puis signes écrits/notation numérique au moment de l’apprentissage de la lecture et de l’écriture).

L’indépendance fonctionnelle de ces systèmes est attestée depuis plusieurs années déjà par diverses études dans la population typique (chez l’adulte : Dehaene et Cohen, 1995 ; Dehaene et coll., 1998 et 1999 ; chez l’enfant : Temple et Posner, 1998).

Le modèle de cognition numérique, proposé par Stanislas Dehaene (1992), constitue un cadre de référence largement reconnu dans le monde scientifique (Camp et coll., 2011). Il détaille les composantes du système analogique et les composantes du système de représentation symbolique. Il permet également de faire le lien avec des catégories de tâches qui requièrent de façon plus ou moins prépondérante certains de ces processus (figure 11.2).

Le système analogique fait appel à deux processus :

• le processus de subitizing qui est une sensibilité précoce à la numérosité de petits ensembles d’objets grâce à un mécanisme de saisie perceptive globale. Ce mécanisme permet d’évoquer la cardinalité3 d’une collection jusqu’à 3 éléments de façon immédiate et très précise (Kaufman et coll., 1949). Il permet aussi de comparer et de discriminer des petits arrangements dont la numérosité varie (1 versus 2 versus 3, par exemple). Il repose sur un système spécifique de saisie visuelle instantanée de la collection sous forme d’objet ou de configuration dit Object-Tracking System (OTS) ;

• le processus d’estimation qui renvoie à l’appréhension approximative de la numérosité de collections d’objets dès 4 éléments. Le processus d’estimation, comme le processus de subitizing, est fonctionnel dès le début de la vie chez l’homme4 . Il permet de comparer et de discriminer des ensembles numériquement importants, apparemment sans limite de taille, mais ne permet pas de répondre de façon exacte aux questions commençant par « combien de » (par exemple combien d’éléments cette collection contient-elle ?). Le processus d’approximation obéit à la loi dite « fraction de Weber », qui suppose que le temps requis pour comparer deux collections dépend non de la valeur réelle mais de leur ratio (Moyer et Landauer, 1967 ; Dehaene et coll., 1990). Autrement dit, cette loi stipule qu’il est plus facile et plus rapide de conclure à la différence numérique entre deux collections, si la différence numérique entre les ensembles à comparer est importante. On qualifie cette aptitude d’acuité numérique. L’acuité numérique se calcule sous la forme d’un pourcentage minimal discriminé (Dehaene, 2010). Avec le développement, elle devient possible même lorsque les collections sont numériquement très proches. Elle est d’environ 1 :2 (100 %) à six mois, de 2 :3 à 10 mois et de 7 :8 à l’âge adulte (Feigenson et coll., 2004 ; Halberda et coll., 2008). La littérature montre que, dans la population typique, les habiletés d’acuité numérique corrèlent avec les performances mathématiques ultérieures (Halberda et coll., 2008 ; Mazzocco et coll., 2011), ce qui confirme le rôle décisif de ce mode de représentation dans le niveau de maîtrise atteint ultérieurement en numératie (Camp et coll., 2011 ; Libertus et coll., 2011).

Le système de représentation symbolique des nombres se développe sous l’influence de la culture. C’est-à-dire qu’il s’apprend à l’école, dans le cadre familial, etc. L’apprentissage suppose l’intégration des signaux linguistiques et des systèmes de notation utilisés pour évoquer les nombres dans la culture d’appartenance (chiffres arabes, chiffres romains, mots-nombre formulés verbalement, lus ou écrits, etc.). Le système symbolique est formé de deux sous-composantes :

• le processus de décodage, de manipulation et/ou de production des motsnombre (/trois/ ; /dix-huit/ ; etc.) d’une part ;

• le processus de décodage, de manipulation et/ou de production des chiffres arabes (1, 44, 1000, etc.) d’autre part.

La coordination des deux systèmes – analogique et symbolique – est requise dans les habiletés mathématiques complexes. La maîtrise du comptage, de même que la possibilité de se représenter une numérosité à partir d’une indication chiffrée écrite ou orale, par exemple [12] ou /douze/ seront ainsi compromises en cas de dysfonctionnement de l’un ou l’autre des deux systèmes (Ostergren, 2013).

La mobilisation des systèmes analogique et symbolique varie selon les catégories de tâches (Kucian et coll., 2008).

En règle générale, les tâches de comparaison de magnitudes, tout comme celles de calcul approximatif, requièrent seulement la discrimination quantitative qui repose sur le système analogique des quantités5 . La représentation des magnitudes serait spatialisée. Elle s’appuierait sur une ligne mentale horizontale qui se déroulerait de gauche à droite (Dehaene et coll., 2003 ; Hubbard et coll., 2005 ; Bonato et coll., 2012). Cette ligne numérique mentale renverrait à un continuum sur lequel les quantités, puis les nombres, seraient représentés en fonction de leur importance respective (Kyttälä, 2008). Une telle représentation serait également activée dans l’estimation et l’approximation des durées, ainsi que dans la comparaison et finalement la sériation des événements temporels (Thioux et coll., 2005).

Le rappel des faits arithmétiques (tables d’addition et de multiplication, par exemple) s’appuie principalement sur le système verbal (ou auditif) du système symbolique (Campbell, 1994 ; Spelke et Tsivkin, 2001). Il fait appel à la mémoire à long terme.

Les tâches d’addition sont médiatisées par les voies verbales (ou auditives, système symbolique) du comptage et des faits numériques, a contrario la soustraction mobilise la représentation analogique des magnitudes (Kucian et coll., 2008 ; Prado et coll., 2014).

L’activité de dénombrement (ou comptage) nécessite quant à elle l’intégration des deux systèmes. En effet, elle demande la mise en correspondance systématique entre chacun des objets d’une collection et un élément correspondant dans l’ensemble de référence (par exemple la suite des nombres, doigts de la main, etc.). Le comptage exact d’objets est tributaire de la compréhension du principe de cardinalité6 . Il arrive cependant parfois que le dénombrement opère principalement par le biais du système de représentation analogique, par exemple, lorsque l’enfant s’appuie sur une collection de référence concrète telle que les doigts de la main.

Les difficultés rencontrées par les personnes avec une DI en numératie sont souvent partiellement spécifiques au syndrome considéré (Cornish et coll., 2007). Elles ne peuvent pas être comprises, ni interprétées, comme de simples retards sur la trajectoire développementale classique.

Les faiblesses peuvent être consécutives à des perturbations dans les processus cognitifs généraux comme par exemple des perturbations touchant la MdT, les fonctions exécutives, etc. Elles peuvent être liées à des troubles des processus numériques spécifiques (subitizing, estimation, processus de représentation symbolique) (Simon, 2011). Plus souvent, elles résultent de l’interaction entre ces deux types de processus (De Smedt et coll., 2009).

Dans une revue de littérature récente, Camp et coll. (2011) constatent qu’il y a moins de 20 études publiées concernant les habiletés numériques des personnes avec un SW, ceci malgré le fait « que la cognition numérique représente (à l’évidence) un domaine dans lequel les habiletés [de ces personnes] sont faibles » (p. 302). Dans ce syndrome, le processus de subitizing est généralement préservé (Paterson, 2001 ; Paterson et coll., 2006). Van Herwegen et coll. (2008) rapportent que les enfants (entre 13 et 53 mois et avec un âge mental entre 22 et 38 mois), avec un SW, manifestent des compétences d’estimation exacte des petites collections (>3 éléments) comparables à celles de pairs d’âge chronologique équivalent. En revanche, les travaux scientifiques montrent que l’estimation de la « numérosité de collections plus importantes » leur pose des difficultés (Ansari et coll., 2007 ; Van Herwegen et coll., 2008 ; Krajcsi et coll., 2009), ceci même lorsque les ensembles sont numériquement très contrastés (ratio 1 :2). Dans ce public, la représentation de la ligne numérique est déficitaire (Paterson et coll., 2006 ; O’Hearn et Landau, 2007). Rousselle et coll. (2013) confirment les observations précédentes, signalant toutefois que les déficits dans le « traitement des magnitudes » concernent uniquement les magnitudes numériques et spatiales, et non la magnitude temporelle (comparaison de la durée de sons).

La récitation de la « comptine »7 est fluide, mais elle plafonne très vite et rares sont les participants qui parviennent à énoncer la suite des nombres au-delà de 25 (Paterson et coll., 2006). Alors qu’ils ont de la facilité à réciter la comptine dans l’ordre, les enfants avec un SW rencontrent des difficultés dans des tâches nécessitant un va-et-vient sur la ligne numérique. Ils sont en difficulté lorsqu’il s’agit de réciter la comptine dans le sens inverse, de l’énoncer à partir d’un nombre supérieur à 0, de répondre à des questions comme « Qu’est-ce qui vient avant/après x, y ou z ? » ou encore lorsqu’ils doivent réaliser une tâche de sériation avec des stimuli analogiques ou des nombres arabes. Si la lecture de chiffres ayant une graphie simple (0 à 9) est réussie sans erreur, la performance chute face aux chiffres complexes (Paterson et coll., 2006). Une telle difficulté n’est cependant pas retrouvée par O’Hearn et Landau (2007).

L’apparition du principe de « cardinalité »8 est tardive (Ansari et coll., 2003). Une fois ce principe acquis, le comptage reste lent, car les personnes avec un SW ont besoin de plus de temps pour dénombrer les éléments d’une collection (Krajcsi et coll., 2005 et 2009). Le comptage s’accélère avec l’âge et l’entraînement, mais au détriment souvent de la précision et de la justesse de la réponse (O’Hearn et coll., 2011). Le niveau de compréhension de la cardinalité peut être prédit par les compétences visuo-spatiales. Ansari et coll. (2003) observent que les enfants avec un SW (entre 6 et 11,5 ans) obtiennent des performances comparables à celles des enfants tout-venant appariés sur leurs habiletés visuo-spatiales. Les difficultés de compréhension de la cardinalité sont plus marquées chez les enfants avec SW ayant un niveau de langage verbal inférieur à 4 ans 8 mois.

O’Hearn et Landau (2007) confirment les difficultés des personnes avec SW à mettre en place la ligne numérique mentale, mais relèvent leurs ressources en ce qui concerne les compétences numériques verbales. Après examen des performances mathématiques de 14 jeunes (âge moyen 17 ans 9 mois, ± 7,3) appariés à des enfants tout-venant d’âge mental équivalent (âge moyen 6 ans 2 mois, ± 1,1) à l’aide de la batterie TEMA-2 (Test of Early Mathematical Ability), ils observent que les participants avec SW obtiennent de meilleurs résultats que les témoins aux tâches de « lecture de chiffres » ainsi qu’en ce qui concerne la « mémoire des faits mathématiques ». Ils concluent à la possibilité d’atteindre pour certains, des performances de niveau CE2 (O’Hearn et Landau, 2007 ; O’Hearn et Luna, 2009). Les habiletés numériques verbales masquent souvent les difficultés conceptuelles, ce qui conduit l’entourage à les sous-estimer.

Sur le plan fonctionnel, une fois devenus adultes, la « maîtrise de l’argent » est particulièrement problématique pour la plupart des personnes concernées (Bellugi et coll., 2000), il en va de même de la capacité à se situer dans le temps (Davies et coll., 1997).

Les difficultés mathématiques que rencontrent les personnes avec un SW peuvent résulter d’un fonctionnement atypique du sous-système approximatif – approximatif-analogique chez Dehaene – de représentation du nombre9 (Libertus et coll., 2014). Elles sont aussi tributaires de difficultés que rencontrent ces personnes dans les systèmes cognitifs plus généraux, comme par exemple dans le système visuo-spatial et spatial. La réalisation des tâches d’estimation est impactée par des difficultés d’attention spatiale et de déplacement du regard (Van Herwegen et coll., 2008). À l’instar d’autres syndromes comme par exemple le syndrome 22q11.2 (Simon et coll., 2005), les difficultés de navigation sur la ligne numérique rencontrées par les personnes avec un SW peuvent s’expliquer par un dysfonctionnement du système visuo-spatial (voir O’Hearn et coll., 2011 pour une synthèse).

La numératie est un domaine peu documenté et le profil de forces et faiblesses des personnes avec trisomie 21 (T21) en mathématique reste encore mal connu (Brigstocke et coll., 2008). Dans tous les chapitres consacrés aux personnes avec une T21 (Dykens et coll., 2000 ; Holmes, 2010 ; Farran et Karmiloff-Smith, 2012), seul le manuel de Faragher et Clarke (2014) aborde ce domaine de fonctionnement. Ceci s’explique peut-être par le fait que les difficultés langagières rencontrées par les personnes avec une T21 monopolisent davantage l’attention ou parce qu’en comparaison à d’autres syndromes (comme le syndrome de Williams), les personnes avec T21 se montrent plus performantes sur le plan des habiletés mathématiques (Paterson et coll., 2006).

Les observations empiriques témoignent d’un déficit dans le processus de subitizing. Paterson et coll. (2006) rapportent que les enfants avec T21 de 2-3 ans peinent à discriminer des ensembles composés de 2 versus 3 éléments. Des observations analogues ont été rapportées par Sella et coll. (2013) chez des jeunes de 14 ans en comparaison d’enfants typiques (±5,5 ans) appariés sur l’âge mental. En ce qui concerne le « processus d’estimation » (= sous-système d’approximation) utilisé pour quantifier la numérosité de collections plus importantes, Sella et coll. (2013) rapportent des habiletés d’estimation plus faibles que les pairs de même âge chronologique, mais comparables à celles du groupe contrôle apparié sur l’âge mental. Camos (2009), qui a observé chez des enfants avec T21 de 6 ans quant à elle, conclut à des habiletés préservées non seulement en comparaison d’enfants de même âge mental, mais aussi d’âge chronologique équivalent. L’effet de distance10 semble tout aussi marqué chez les personnes avec une T21 (entre 11 et 35 ans) que dans les groupes contrôle appariés sur l’âge chronologique et celui de développement ce qui confirme une habileté préservée à naviguer sur la ligne numérique (Paterson et coll., 2006). Ces études montrent donc un décalage en défaveur des personnes avec T21 par rapport aux typiques pour ce qui est du subitizing (collections numériquement faibles), mais non des opérations d’approximation sur des collections numériquement plus importantes.

En comparaison d’enfants typiques appariés sur l’âge chronologique et développemental, la récitation de la « comptine numérique » est moins fluide (Nye et coll., 2001 ; Sella et coll., 2013). Camos (2009) considère qu’une des sources les plus probables des difficultés observées se situe au niveau de l’apprentissage et de la maîtrise des sous-systèmes symboliques arabe et verbal – et de la coordination de ces connaissances avec celles du système analogique – qui est à la base de toutes les habiletés mathématiques ultérieures. La maîtrise de la comptine semble plafonnée. Ces conclusions corroborent celle de l’étude de Paterson et coll. (2006), où les participants adolescents et personnes adultes manifestaient une bonne maîtrise de la suite des nombres jusqu’à 35, leurs performances diminuaient au-delà.

En ce qui concerne la « cardinalité », les observations sont contradictoires. Plusieurs études récentes rapportent que le principe de cardinalité serait préservé chez les personnes avec une T21 (Caycho et coll., 1991 ; Nye et coll., 2001 ; Paterson et coll., 2006 ; Sella et coll., 2013) contrairement à certains travaux plus anciens qui font état d’une grande variabilité au sein de ce groupe clinique (Gelman et Cohen, 1988). En ce qui concerne la compréhension du zéro, une seule étude, celle de Noda Herrera et coll. (2011), aborde ce thème. Dans cette recherche, douze participants avec T21 (entre 12 et 31 ans) ont été invités à résoudre des additions et des soustractions d’une part, et à expliquer leur procédure et les résultats obtenus d’autre part. Les résultats montrent que les participants comprennent le zéro comme une absence d’objets et non comme la conséquence d’une procédure algorithmique. Ce faisant, cette étude montre que si les opérations sont maîtrisées, la compréhension des principes mathématiques qui les sous-tendent n’est pas nécessairement complète.

L’influence du soutien n’a été évaluée que par Nye et coll. (2001). Dans cette étude, les compétences procédurales de comptage (avec et sans soutien parental), de même que la compréhension conceptuelle de la cardinalité de 23 enfants avec T21 (entre 3,5 et 7 ans) sont comparées à 20 enfants (entre 2 et 4 ans) typiques, appariés sur l’âge mental non-verbal (âge mental entre 2,5 et 4 ans). Il a été demandé aux enfants de dénombrer des jouets dans des collections comprenant entre 2 et 18 items (mesure des compétences procédurales de comptage) ; de prélever sur consigne un nombre d’objets à l’intérieur d’une collection pour les donner à un tiers (mesure de la compréhension de la cardinalité) et de réciter la comptine numérique oralement, pour évaluer la production de séquence indépendamment du comptage d’objets. Les enfants avec développement typique ont récité significativement plus de nombres au total, ont produit des séquences numériques plus longues et ont réussi à dénombrer des ensembles plus grands que les enfants avec une T21. Le soutien d’un adulte améliore significativement la performance des participants à la tâche de comptage. Cet effet est présent dans les deux groupes. Les enfants avec T21 ne se différencient pas des enfants typiques en ce qui concerne les stratégies utilisées pour résoudre la tâche. Cette étude montre, comme précédemment, une compréhension de la cardinalité intacte.

La numératie est l’un des domaines dans lesquels les personnes atteintes de microdélétion 22q11.2, enfants comme adultes, sont susceptibles de rencontrer des difficultés significatives. Tous les processus ne sont cependant pas également touchés. Le « rappel de faits numériques », la « capacité à dénombrer des collections de petite taille (< 3) » et la « lecture et l’écriture de chiffres » sont épargnés (Simon et coll., 2005 ; De Smedt et coll., 2006). Les difficultés concernent plus particulièrement la « représentation des collections de grande taille (> 3) », la « comparaison des magnitudes » (longueur, nombre), les calculs et les « opérations simples », ainsi que, dans une certaine mesure, les exercices dits « situations-problèmes » (De Smedt et coll., 2007, 2008 et 2009).

Simon et coll. (2005) observent que les enfants avec une microdélétion 22q11.2 (entre 7 et 14 ans) peinent à évaluer la distance entre les nombres, que ceux-ci soient présentés sous forme analogique (« Y a-t-il plus [d’éléments] que ? » ; « moins [d’éléments] que ? ») ou sous forme symbolique dans le système de notation arabe (« Ce nombre est-il plus grand que ? » ; « plus petit que ? »). Faire des distinctions plus subtiles leur est difficile, comme si les dysfonctionnements visuo-spatiaux décrits généraient une représentation de la magnitude ayant une capacité de résolution plus faible et moins détaillée (Simon, 2008). Les individus avec une microdélétion 22q11.2 se montrent donc moins performants et moins précis dans la discrimination de quantités et dans l’estimation de magnitudes, signant une « navigation » déficitaire sur la ligne numérique mentale (De Smedt et coll., 2006, 2007 et 2008). Des difficultés dans le comptage sont relevées par certains auteurs (Simon et coll., 2005 et 2008), mais pas par tous (De Smedt et coll., 2008).

De Smedt et coll. (2008) rapportent une aptitude réduite à résoudre des « additions » et des « soustractions » avec retenue chez 25 enfants avec une microdélétion 22q11.2 (entre 6 et 12 ans) comparés à 25 enfants d’âge et de sexe équivalent et scolarisés dans la même classe. Les résultats à ces opérations contrastent avec les bonnes capacités observées dans le rappel des faits numériques. Ces observations sont convergentes avec celles d’Eliez et coll. (2001) qui ont comparé huit adolescents avec une microdélétion 22q11.2 (âge moyen : 15,5 ans) à huit adolescents typiques dans une tâche de raisonnement mathématique. La tâche consistait à vérifier les résultats, tantôt corrects, tantôt incorrects, proposés en réponse à des problèmes additifs ou soustractifs, respectivement faciles versus difficiles. Une augmentation atypique de l’activité neuronale a été observée chez les individus ayant une microdélétion 22q11.2 face aux tâches difficiles, c’est-à-dire faisant appel à des algorithmes de résolution en comparaison des tâches requérant « simplement » des informations apprises par cœur et stockées en mémoire. Les personnes avec une microdélétion 22q11.2 sont mises à rude épreuve dès l’apparition d’exigences scolaires demandant la maîtrise de procédures dans les opérations arithmétiques (De Smedt et coll., 2009).

Les difficultés mathématiques que rencontrent les personnes avec une microdélétion 22q11.2 sont de nature principalement procédurale (De Smedt et coll., 2008). Différentes explications sont avancées (voir De Smedt et coll., 2009 pour une synthèse). Elles peuvent résulter d’un fonctionnement atypique du sous-système approximatif (De Smedt et coll., 2006). Il est aussi possible qu’elles résultent de dysfonctionnements intervenant au niveau des sous-systèmes cognitifs généraux. On sait en effet que le fonctionnement intellectuel des personnes avec une microdélétion 22q11.2 se caractérise par un déséquilibre entre le QI de performance et le QI verbal en faveur de ce dernier (Moss et coll., 1999 ; De Smedt et coll., 2008)11 et que les systèmes visuo-spatial et exécutif sont fréquemment dysfonctionnels (Antshel et coll., 2008 ; Jacobson et coll., 2010 ; Campbell et coll., 2010 ; Lepach et Petermann, 2011). Henry et coll. (2002) rapportent par exemple des difficultés de planification dont on peut penser qu’elles ne sont pas sans conséquences sur la procédure de résolution des situations-problèmes. Finalement, les difficultés à reformuler un propos constatées par Persson et coll. (2006), sont elles aussi susceptibles de compliquer la résolution de problème en parasitant l’activité de reformulation de la consigne ou de l’énoncé. Les difficultés que rencontrent les personnes avec une microdélétion 22q11.2 en mathématiques semblent ne pas pouvoir s’expliquer par un dysfonctionnement de la MdeT (De Smedt et coll., 2008).

On dispose actuellement de meilleures connaissances sur les mécanismes cognitifs de base sous-tendant les compétences numériques dans le fonctionnement typique et atypique (Dehaene et Cohen, 1995 ; Dehaene et coll., 1998 et 1999 ; Camp et coll., 2011 ; chez l’enfant : Temple et Posner, 1998). Dans la population ayant une DI, les résultats des études syndromiques montrent que :

• le fonctionnement mathématique des personnes concernées n’est pas uniformément déficitaire : certaines pathologies, par exemple le syndrome de Williams, la trisomie 21, le syndrome velo-cardio-facial, etc., peuvent affecter plus particulièrement certains processus et en épargner d’autres, donnant lieu à des profils de compréhension mathématique particuliers (tableau 11.II) ;

• un même profil cognitif peut se retrouver dans plusieurs syndromes (Dykens et coll., 2000 ; Mazzocco, 2007).

Actuellement, la compréhension de ces profils de forces et de faiblesses ne concerne encore qu’un nombre très limité de syndromes (Hodapp et coll., 2003). La compréhension du fonctionnement des personnes ayant une DI idiopathique dans le domaine des mathématiques n’est pas aussi avancée que celle des populations atteintes d’un syndrome mieux délimité. Les auteurs s’accordent sur le fait que les données issues des études syndromiques peuvent actuellement servir de modèles pour la compréhension des troubles dans d’autres conditions cliniques (Mazzocco, 2007). Pour cette raison, il est nécessaire de ne pas cloisonner les corpus de connaissances.

Les chercheurs et les praticiens intéressés par ces différents sous-groupes devraient unir leurs forces et leurs connaissances respectives (Dykens et coll., 2000).

Que savons-nous de la progression et du niveau de performance pouvant être atteints par les personnes avec une DI ? Nous avons cherché des indications permettant de répondre à cette question à partir de deux sources de données issues d’études nationales et internationales mesurant les performances scolaires d’une part, et d’études longitudinales d’autre part.

Depuis quelques décennies, les pays occidentaux se sont dotés de moyens visant à évaluer les performances de leurs systèmes éducatifs (enquêtes de l’IEA – International Association for the Evaluation of Educational Achievement ; enquêtes PISA – Programme international pour le suivi des acquis des élèves). Ils recourent pour cela à des enquêtes à grande échelle menées périodiquement. L’objectif est de tester les acquis scolaires des élèves d’un certain groupe d’âge et de collecter des informations contextuelles. Il ne s’agit pas de situer l’élève de façon individuelle, mais d’obtenir certaines indications concernant des sous-groupes d’élèves en fonction de certaines caractéristiques (performance selon le sexe, le milieu socio-économique, etc.). Cependant, le public avec une DI, enfants comme adultes, est exclu de ces grandes enquêtes internationales. Schuelka (2013) considère cette mise à l’écart comme problématique dans le sens où elle marginalise la voix du public concerné et le laisse en dehors des réflexions et des décisions socio-politiques en matière d’éducation.

La récente étude internationale de l’OCDE sur les compétences académiques des adultes est emblématique de ce phénomène car elle s’adresse uniquement aux résidants tout-venant âgés de 16 à 65 ans, qui dans les pays participants ne sont pas institutionnalisés. Il en est de même des études PISA menées tous les 3 ans par l’OCDE destinées à évaluer de façon périodique, les connaissances et les compétences en littéracie, en numératie et en sciences des élèves de 15 ans. Dans ces études, les consignes d’administration n’autorisent, ni ne prévoient l’activation de dispositifs de soutien. Cette manière de procéder a pour conséquence une exclusion presque systématique des élèves ayant des besoins éducatifs particuliers, dont les élèves avec une DI. Les principes de recrutement prévoient par ailleurs que :

• les établissements spécialisés ne participent pas à l’enquête ;

• les élèves ayant des besoins éducatifs particuliers intégrés en milieu scolaire ordinaire ne participent à l’enquête que si l’établissement scolaire considère que le jeune est en mesure d’y participer (voir OCDE, 2011, p. 26 pour une explication concernant les critères définissant la population cible et les élèves exclus).

Depuis 2003, un cahier simplifié a été développé à l’intention des élèves exclus de l’enquête car fréquentant un établissement spécialisé. Ce cahier contient une partie seulement des items de la batterie standard avec une durée de passation de l’épreuve plus courte (une heure à la place de deux pour ne pas solliciter excessivement les ressources attentionnelles). Il permet une évaluation parallèle à l’évaluation PISA. Cependant, cette évaluation est optionnelle. En 2003, 26 des 30 pays membres de l’OCDE l’ont appliquée. Ainsi, 1 815 élèves ayant des besoins éducatifs particuliers, soit 0,66 % de l’échantillon total, ont pu participer. Pour des raisons non communiquées, la France n’a pas mis en œuvre ce volet de l’évaluation (OCDE, 2003). Les données recueillies dans les pays ayant introduit la mesure simplifiée sont de faible utilité pour la mesure de l’accomplissement en numératie des personnes avec une DI. En effet, les données se présentent sous une forme trop agrégée pour être exploitable. L’OCDE regroupe les données nationales en trois catégories transnationales très globales qui ne permettent pas d’identifier les élèves avec une DI à l’intérieur des élèves ayant des besoins éducatifs particuliers (BEP)13 . La typologie utilisée par l’OCDE (2000, 2008) comprend en effet les trois grandes catégories suivantes :

• catégorie transnationale « A/Déficiences ». Cette catégorie concerne les élèves présentant des déficiences ou incapacités considérées du point de vue médical comme des troubles d’origine organique (liés par exemple à des déficiences sensorielles, motrices ou neurologiques). Le besoin éducatif résulterait principalement de difficultés imputables aux déficiences mentionnées ;

• catégorie internationale « B/Difficultés ». Cette catégorie concerne les élèves présentant des troubles du comportement, des troubles affectifs ou des difficultés spécifiques d’apprentissage. Le besoin éducatif résulterait principalement de difficultés d’interaction entre l’élève et l’environnement éducatif ;

• catégorie internationale « C/Désavantages ». Cette catégorie concerne les élèves présentant des désavantages découlant principalement de facteurs socio-économiques, culturels et/ou linguistiques. L’intervention consisterait principalement à compenser les désavantages imputables à ces facteurs.

Les personnes avec une DI font ainsi partie de la catégorie transnationale A au même titre que les personnes concernées par une déficience physique, une déficience sensorielle (auditive et visuelle), des troubles du métabolisme, des troubles neuro-psychologiques, des troubles du langage et de la parole, des « handicaps multiples ou encore des déficiences non spécifiées » (OCDE, 2003). Une telle agrégation rend les données issues des enquêtes internationales inexploitables.

Certains pays procèdent à des enquêtes similaires. L’évaluation est réservée aux élèves scolarisés sur le territoire national, l’enquête visant à monitorer les résultats scolaires à l’échelon national. Des dispositifs sont parfois prévus pour favoriser la participation des élèves ayant des besoins éducatifs particuliers. Ceux qui ne sont pas en mesure de participer à l’évaluation nationale sont soumis à une évaluation alternative14 (Karvonen et coll., 2013). Les États-Unis par exemple proposent trois formes d’évaluation alternative, dont l’une s’adresse spécifiquement aux élèves décrits comme ayant des difficultés cognitives significatives (voir le descriptif du National Center on Educational Outcomes-NCEO15 ). Cette opportunité n’est jusqu’ici utilisée que par le Missouri sur l’ensemble des États américains (Albus et Thurlow, 2013). À terme toutefois, cette manière de procéder devrait permettre de mieux intégrer cette catégorie d’élèves et de renforcer la responsabilité du système éducatif à leur égard.

Les études longitudinales constituent la seconde source d’information susceptible de permettre de répondre à la question du niveau de performance atteint par les personnes avec une DI en numératie.

Bien que rares et datées, ces études livrent d’utiles informations. Turner et Alborz (2003) ainsi que Turner et coll. (2008) rapportent les résultats d’un suivi longitudinal entre 1986 et 2000, impliquant 71 enfants, adolescents et jeunes adultes (9-21 ans) avec une T21, parmi lesquels 90 % des enfants et leurs familles sont de la région du Grand Manchester. Les compétences en numératie et en littéracie ont été mesurées à trois moments au cours de la vie des participants, soit à 9, 14 et 21 ans. Les auteurs rapportent qu’au seuil de l’âge adulte :

• 75 % des participants maîtrisent une partie des habiletés de degré préscolaire dans le domaine de la lecture, de l’écriture et du nombre ;

• 50 % maîtrisent également certaines compétences de niveau CP à CE1 dans les trois domaines ;

• 25 % parviennent à maîtriser certaines habiletés scolaires de niveau CE2 à CM2 dans les trois domaines, c’est-à-dire des habiletés habituellement enseignées aux élèves entre 7 et 11 ans et, dans le domaine numérique seulement, des habiletés de niveau secondaire, c’est-à-dire enseignées aux élèves de 6^e à 3^e (11 à 14 ans).

En ce qui concerne les facteurs d’influence, les auteurs observent que le niveau de performance atteint est très fortement prédit par la sévérité de la DI. Cette variable n’est cependant pas le seul prédicteur en jeu : des facteurs individuels tels que le genre ou le niveau d’attention de l’élève influencent aussi le niveau de performance atteint en lecture, écriture et mathématiques. De même, des variables contextuelles, sociales (par exemple une scolarisation dans un environnement moins restrictif) et familiales (comme le niveau de formation de la mère, sa capacité à faire face aux difficultés rencontrées, etc.) agissent également de façon significative. Considérés ensemble, les facteurs indiqués parviendraient à expliquer 48 % de la variance des résultats scolaires des jeunes adultes avec T21.

L’influence de l’instruction sur le niveau de performance en mathématique auquel peuvent prétendre les personnes avec une DI est corroborée par d’autres études. La méta-analyse de Browder et coll. (2008) conclut à des gains d’apprentissage importants (en anglais large) suite à des interventions en numératie auprès de personnes ayant une DI modérée ou sévère. Le constat des auteurs s’appuie sur 68 études répondant toutes aux exigences méthodologiques des pratiques fondées sur les preuves (Evidence based practices) et impliquant au total 493 personnes. En 1994, Shepperdson avait déjà constaté un niveau de performance scolaire significativement meilleur dans une cohorte née en 1970 ayant reçu plus d’attention sur le plan pédagogique en comparaison d’une cohorte née en 1960. Finalement, la progression des compétences académiques – notamment en lecture – sous l’effet de l’instruction est observée tant chez les enfants avec T21 (Rynders et coll., 1997), que dans un échantillon composé d’enfants avec une DI d’étiologie et de sévérité variées (Beadle-Brown et coll., 2000). Les études longitudinales rapportent des gains d’apprentissage chez les personnes adultes attestant ainsi de la progression continue au-delà de la période scolaire (Rynders et coll., 1997). Dans une étude plus récente visant les performances en mathématiques d’élèves malvoyants d’âge scolaire avec et sans déficience cognitive, Giesen et coll. (2012) rapportent que la présence de troubles cognitifs ne bloque pas la progression en mathématiques. Ils constatent qu’un soutien intensif et spécialisé doit cependant être proposé aux élèves concernés pour leur permettre de continuer à progresser.

Les travaux mentionnés ci-dessus portent sur des publics dont le parcours scolaire a pris place à une époque où l’enseignement des savoirs académiques était encore réduit en raison de faibles attentes éducatives et d’une inclusion scolaire balbutiante (Kliewer et coll., 2006). Cet état de fait est susceptible de conduire à une sous-estimation du niveau de compétence pouvant être atteint par les élèves avec une DI dans les acquisitions scolaires. Sous l’influence des principes d’« éducation pour tous », on peut raisonnablement croire que le niveau moyen de compétence des personnes avec une DI scolarisées et bénéficiant d’opportunités d’instruction a dû ou va encore augmenter (Turner et Alborz, 2003).

Aux États-Unis, quinze ans après l’introduction de la loi IDEA16 instituant la scolarisation des élèves avec des besoins éducatifs particuliers dans les milieux plus ouverts à l’inclusion et un accès égal aux contenus académiques, Karvonen et coll. (2013) ont évalué l’accès des élèves avec une déficience intellectuelle au programme d’étude17 régulier. En ce qui concerne les mathématiques, les résultats montrent que le niveau d’accès est influencé par l’attitude de l’enseignant vis-à-vis des mesures inclusives et par les caractéristiques de l’élève, notamment son niveau de communication. Les élèves ont, soit un accès limité au plan d’étude, soit un accès ciblé sur les contenus mathématiques, soit enfin un accès large au plan d’étude, avec accès à différentes matières. Leurs performances sont corrélées à leur niveau d’accès : elles sont faibles pour les élèves ayant un accès limité, moyenne chez ceux qui ont un accès ciblé et élevées chez ceux qui ont un accès large. En ce qui concerne les caractéristiques de l’enseignant, les auteurs rapportent que la référence au curriculum est prédite par les connaissances sur les stratégies d’apprentissage dont dispose l’enseignant et sa capacité à activer des moyens lui permettant d’évaluer régulièrement la progression de l’élève. Sa formation dans le domaine des mathématiques, son expérience d’enseignement avec des élèves ayant une DI ou en mathématiques, le matériel pédagogique à sa disposition, le degré scolaire dans lequel il enseigne, ne jouent pas de rôle sur la manière dont il se réfère (ou non) au curriculum régulier.

En résumé, la maîtrise de la numératie est cruciale pour la qualité de vie des personnes avec une DI comme pour toute autre personne (Faragher et Brown, 2005).

Les données longitudinales disponibles indiquent qu’il ne faut pas sous-estimer la capacité de ces personnes à progresser dans la maîtrise des habiletés numériques (Beadle-Brown et coll., 2000 ; Turner et Alborz, 2003 ; Turner et coll., 2008). Des progrès peuvent être attendus au-delà de l’âge scolaire (Rynders et coll., 1997). Un tel constat justifie de soutenir les apprentissages tout au long de la vie.

Le niveau de performance atteint par un individu dépend principalement de ses aptitudes intellectuelles et de la possibilité pour lui de recevoir une instruction dans le domaine concerné (Browder et coll., 2008). La marge de progression des élèves avec une DI, sous l’effet des conditions éducatives actuelles, devrait cependant être davantage étudiée. En effet, les informations disponibles restent imprécises et difficilement exploitables en raison d’une insuffisance de données, de données datées, d’une trop grande agrégation des résultats et/ou d’une absence de volonté politique de veiller au recueil régulier et exhaustif de ces données (Albus et Thurlow, 2013 ; Schuelka, 2013). Afin de disposer d’études permettant de rendre compte de façon plus précise de la marge de progression des personnes avec une DI en mathématiques et de leur variabilité interindividuelle, il est nécessaire d’encourager la recherche longitudinale. Celle-ci devrait s’appuyer sur des dispositifs d’évaluation répondant aux principes de « conception universelle18  », c’est-à-dire utilisables par le plus grand nombre (Karvonen et coll., 2013 ; Schuelka, 2013).

L’évaluation des habiletés mathématiques peut se faire à l’aide de deux types d’outils.

D’une part, à l’aide des batteries étalonnées s’appuyant sur les modèles théoriques développés en psychologie ou en neuropsychologie19 . Toutefois, ces outils ont été principalement utilisés et développés pour un public sans DI. Certains sont disponibles en langue française. Leur administration chez des personnes ayant une DI n’étant pas encore documentée, leur utilisation nécessitera peut-être de : rendre accessible le dispositif dont l’ergonomie peut se révéler non adaptée au public testé ; veiller à l’effet plancher en évitant les dispositifs trop difficiles pour le public testé ; respecter le principe d’« ageappropriateness ». Ce principe suppose que le dispositif proposé soit accordé autant que possible à l’âge chronologique de la personne testée (Samuel, 1999 ; Forster, 2010). Actuellement, le matériel disponible s’adresse plutôt aux enfants (Smith, 2004).

D’autre part, à l’aide d’instruments mesurant les performances en mathématiques en référence à un plan d’étude donné. Quelques outils de cette catégorie – surtout ceux de langue anglaise – proposent des versions accessibles au public avec des besoins éducatifs particuliers. Une abondante littérature documente les adaptations pouvant être introduites. Des références à ce sujet sont disponibles dans la base de données du NCEO (National Center on Educational Outcomes) sous l’onglet « Accommodations Bibliography » qui recense un grand nombre d’articles publiés sur le thème. Les adaptations documentées concernent le public avec des besoins éducatifs particuliers dans son ensemble, il s’agira donc, en cas de consultation, de vérifier à privilégier les adaptations correspondant aux besoins spécifiques des personnes avec une DI.

Les données sur les programmes d’intervention sont peu nombreuses et diffuses, ce qui limite les réponses aux deux questions suivantes : faut-il enseigner la numératie ? Quelles sont les stratégies les plus efficaces ?

Browder et coll. (2008) ont recensé l’ensemble des études expérimentales et quasi-expérimentales publiées entre 1975 et 2005 ayant mesuré les effets d’interventions menées auprès de personnes avec une DI ou avec un TSA20 dans le domaine de la numératie. Cette méta-analyse a retenu 68 études répondant aux critères d’« Evidence Based Pratice21  », dont 54 plans expérimentaux à cas uniques et 14 études de groupe, soit un total de 493 personnes avec DI incluses, dont une majorité de personnes avec une DI de sévérité modérée. Trente-cinq études impliquaient des participants de niveau lycée (15 à 21 ans), 29 études des élèves de niveau collège (11 à 14 ans), 26 études des élèves de niveaux CP, CE ou CM (6-10/11 ans), 16 études des adultes de plus de 22 ans et 4 études des enfants d’âge préscolaire. Les auteurs constatent que les interventions collectives (documentées par les études de groupe) comme les interventions individuelles (documentées par les études à cas unique) sont efficaces (valeur de la médiane : Cohen’s d = 0,79 pour les premières ; PND = 92,15 pour les secondes). Ils concluent que l’enseignement systématique de la numératie a des effets positifs sur les compétences du public concerné (manipulation des nombres, opérations, mesure, analyse de données représentées graphiquement et de formes géométriques, résolution de situations-problèmes).

Plus récemment, Hord et Bouck (2012) font le même constat. L’analyse de ces auteurs a porté sur les études ciblant l’enseignement des compétences numériques académiques à destination des élèves d’âge scolaire ayant un QI entre 50 et 75. Sur l’ensemble des travaux publiés entre 1999 et 2010, seules sept études répondaient aux critères d’inclusion fixés par les auteurs. Les auteurs soulignent le peu de travaux dans le domaine. Nonobstant la rareté des données, leurs résultats confirment que les élèves avec une DI – ici ceux ayant une DI légère – tirent profit d’un enseignement dans le domaine des mathématiques.

Certains contenus ne sont que rarement enseignés aux personnes avec une DI (Browder et coll., 2008 et 2012 ; Moser-Opitz et coll., 2014). L’analyse de la littérature montre que les interventions sont principalement centrées sur deux grandes familles de contenus, à savoir les opérations arithmétiques élémentaires et la numératie fonctionnelle. Certains auteurs attirent l’attention sur le fait que des attentes réduites, un manque d’ambition ou une absence d’opportunité de se voir proposer des mathématiques complexes peuvent entraver l’accès à l’indépendance des personnes (Browder et coll., 2012) (figure 11.3).

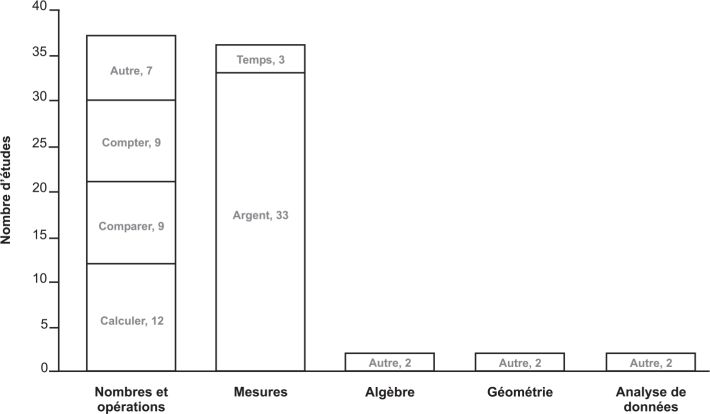
Parmi les études recensées par Browder et coll. (2008), 40,3 % visent l’apprentissage, le perfectionnement et/ou l’entraînement des connaissances relatives aux nombres ou aux opérations mathématiques. 53,7 % visent l’apprentissage ou l’amélioration des habiletés mathématiques fonctionnelles, comme par exemple la manipulation de l’argent ou la connaissance du temps. Les interventions visant des savoirs plus exigeants (enseignement des bases de l’algèbre, de stratégies de résolution de problèmes, procédures d’équivalence, etc.) sont seulement présentes à hauteur de 3 % tout comme les interventions portant sur l’utilisation des connaissances en géométrie et en mathématiques pour mesurer l’espace restent elles aussi exceptionnelles (3 %) et l’enseignement des probabilités (3 %).

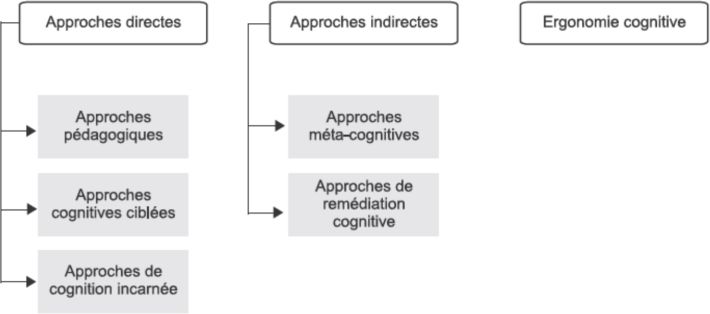
Les interventions avec pour objectif l’amélioration ou le développement des habiletés numériques chez les personnes avec une DI prennent différentes formes. Dans ce qui suit, une distinction sera faite entre les approches intervenant directement sur les habiletés numériques, les approches agissant sur les habiletés et la compréhension numérique par l’entremise d’une action sur d’autres fonctions et finalement les approches ergonomiques mettant l’accent sur l’aménagement de l’environnement (figure 11.4).

Peuvent être considérées comme des approches directes, les approches pédagogiques, les approches cognitives ciblées et les approches de cognition incarnée.

Les approches pédagogiques abordent l’enseignement des mathématiques en référence au curriculum et à la séquence développementale typique. Les objectifs d’apprentissage sont fixés à partir du niveau de performance démontré par l’apprenant en amont de l’apprentissage.

« Effective instruction depends on identifying the knowledge children already possess and building on that knowledge to help them take the next developmental step.Developmental progressions can help identify the next step by providing teachers with a road map for developmentally appropriate instruction for learning different skills22  » (Frye et coll., 2013, p. 12).

Les approches pédagogiques se composent principalement de l’enseignement explicite et structuré, de l’approche constructiviste, ainsi que de l’instruction en contexte réel.

L’enseignement explicite et structuré23 (« skills-based instruction », Kearns et Fuchs, 2013) met l’accent sur le rôle actif de l’enseignant, la transmission explicite des savoirs, ainsi que l’organisation structurée de la matière à enseigner. Les contenus enseignés sont démontrés, décrits et/ou explicités de façon détaillée. La matière est présentée à l’élève selon une logique développementale, par étapes, du plus simple au plus complexe et du concret à l’abstrait. Le feedback, dispensé par l’enseignant, est une stratégie centrale. L’enseignement explicite et structuré est l’approche pédagogique la plus fréquemment mentionnée dans la littérature rapportant les interventions mathématiques à destination des personnes ayant une DI (Browder et coll., 2008 ; Hord et Bouck, 2012). Dans leur revue de littérature sur les interventions à l’intention des élèves ayant une DI légère, Hord et Bouck (2012) observent que sur les 7 études recensées, 6 procèdent par instruction structurée, une seule qui emprunte une approche métacognitive. Les auteurs problématisent ce qui leur paraît être une dissonance entre une pratique très axée sur l’enseignement procédural et les recommandations actuellement préconisées en matière d’enseignement des mathématiques qui mettent l’accent sur la nécessité d’entraîner le raisonnement mathématique et les connaissances de haut niveau. Au terme de leur analyse, Hord et Bouck (2012) invitent les enseignants à ne pas négliger la pensée critique, le raisonnement mathématique et les connexions concrets-abstraits au profit de la mémorisation et des routines. Ces résultats concordent avec ceux de Moser-Opitz et coll. (2014) qui, observant les performances mathématiques d’élèves entre 7,5 et 8,7 ans concluent à la maîtrise de certaines routines mais à l’absence d’habiletés fondamentales telles que le comptage et l’estimation de grandes quantités.

L’enseignement explicite structuré est utilisé pour enseigner une variété de contenus mathématiques, parmi lesquels le comptage, les opérations élémentaires telles qu’addition, soustraction, multiplication et division (Hord et Bouck, 2012), les faits numériques et même parfois, la ligne numérique ou la résolution de problème (Cote et coll., 2011). Aussi bien, Browder et coll. (2008) dans leur méta-analyse, que Gersten et coll. (2009) concluent au fait que l’approche explicite s’accompagne d’effets importants. Il est possible cependant que cette stratégie d’enseignement convienne mieux à certains contenus qu’à d’autres (Wilson et Räsänen, 2009). On sait par exemple qu’elle est bien adaptée à l’apprentissage des faits numériques où elle se révèle plus efficace que l’instruction constructiviste (Kroesbergen et Van Luit, 2005). Pour être efficace, l’approche explicite doit s’accompagner de conditions favorables (opportunités suffisantes d’exercer les compétences, individualisation de l’enseignement, etc.) (Gersten et coll., 2009 ; Vaughn et coll., 2012).

L’approche constructiviste est une pédagogie postulant que l’expérience active de l’apprenant est source d’apprentissage. Elle nécessite de l’enseignant qu’il crée des situations dans lesquelles l’élève peut être actif lui permettant ainsi de construire de nouvelles connaissances par la découverte. L’approche constructiviste, qualifiée de « guided or mediated instruction » en langue anglaise, est quasiment absente de la littérature scientifique consacrée à l’apprentissage des personnes avec une DI. Seuls Kroesbergen et Van Luit (2005) comparent les effets respectifs de l’approche constructiviste et de l’instruction directe lors de l’apprentissage de la multiplication jusqu’à 10 chez des élèves ayant une déficience intellectuelle légère et/ou subnormale. Les groupes non randomisés sont annoncés comme équivalents (QI = 78±3 ; âge chronologique = ±10 ans ; niveau de maîtrise de la procédure de multiplication lors du pré-test). Après 28 leçons, les auteurs observent un gain global de performances dans les deux groupes. Les élèves ayant bénéficié de l’approche structurée se montrent toutefois plus performants que leurs camarades dans les multiplications papier-crayon. Leurs stratégies sont également plus adéquates. D’autres auteurs, dans le cadre de méta-analyses menées auprès d’autres publics (enfants typiques), estiment que l’approche pédagogique constructiviste serait particulièrement efficace dans le cadre préscolaire car elle convient particulièrement bien à l’apprentissage du sens du nombre (Wilson et Räsänen, 2009). Cette efficacité diminuerait au CP (Kroesbergen et Van Luit, 2003 ; Malofeeva, 2005). Dans le champ de la DI, la rareté des études ne permet pas de se prononcer sur l’efficacité de cette approche auprès de ce public.

L’instruction en contexte réel (in vivo) met l’accent sur l’apprentissage par immersion dans les situations de la vie quotidienne. L’apprentissage est qualifié de situé. Dans leur méta-analyse, Browder et coll. (2008) observent que les interventions menées en conditions réelles s’accompagnent d’effets généralement importants. Ce constat est partagé par Xin et coll. (2005) qui ont examiné l’efficacité d’interventions portant sur la manipulation de l’argent dans des tâches d’achat. Ces auteurs ont analysé les publications recensées dans les bases de données ERIC (entre 1978-2003) et PsycLit (entre 1967-2003). Ils sont parvenus à identifier 28 études recourant à des protocoles expérimentaux à cas unique. Les études sélectionnées totalisaient 115 participants âgés de 6 à 74 ans dont la DI variait de sévère à légère. Les résultats de cette méta-analyse montrent que l’enseignement est prioritairement introduit auprès des élèves de niveau secondaire (dès 10 ans) ainsi qu’auprès des adultes. L’efficacité de l’intervention ne serait tributaire, ni de l’âge des apprenants, ni de la sévérité de leur déficience. En ce qui concerne la procédure d’instruction, il n’y aurait pas de différence entre les procédures empruntant la voie de la démonstration, de l’instruction verbale ou celles basées sur l’estompage d’indices qui toutes semblent également efficaces. L’entraînement en situation réelle serait plus efficace que l’entraînement en situation simulée malgré la nécessité d’adaptations comportementales plus complexes comprenant plus d’étapes, dans ces conditions écologiques. Les interventions qui proposent un feedback et une correction des erreurs, soit par signalement verbal, soit par guidance physique, sont plus efficaces que celles qui ne prévoient pas la correction des erreurs. La maîtrise des habiletés de base en mathématiques, de même que la capacité de reconnaître et compter les pièces et les billets et, dans une moindre mesure, une expérience de la communauté constituent des prérequis décisifs pour l’efficacité de l’intervention. Finalement, les résultats montrent un effet important du matériel prothétique (calculette, etc.) sur la maîtrise des comportements attendus. À l’instar de ce qui est considéré chez les personnes tout-venant, on constate donc que l’inscription de l’apprentissage dans un contexte social et culturel facilite l’apprentissage. Une explication réside peut-être dans le fait que les conditions naturelles permettent de donner plus de sens aux contenus appris et soutiennent la dynamique motivationnelle (De Corte et coll., 1996).

En ce qui concerne les autres paramètres des approches pédagogiques, la littérature indique que les conditions suivantes sont susceptibles de faciliter ou au contraire de faire obstacle à l’apprentissage :

• enseignement massé : un enseignement concentré, consistant à vouloir enseigner tout en une seule fois, est peu efficace (Kroesbergen et Van Luit, 2003 ; Browder et coll., 2008) ;

• opportunité de recevoir un feedback : indépendamment des stratégies pédagogiques utilisées, l’apprentissage est optimisé lorsque l’élève a l’opportunité de recevoir un feedback et d’être corrigé lorsqu’il fait une erreur (Browder et coll., 2008) ;

• enseignement collectif versus individuel : parfois, les interventions sont introduites de façon collective (classe, par exemple), d’autres fois elles interviennent dans un cadre individuel (instruction 1 :1) (Browder et coll., 2008). Le peu d’études consacrées aux personnes avec une DI ne permet pas de comparer ces deux conditions ;

• interactions de tutelle (pairs) : en ce qui concerne le public avec une DI, l’enseignement assisté par les pairs n’a pas fait l’objet d’études scientifiques récentes. Les données disponibles concernent seulement les élèves tout-venant24  ;

• enseignement par modelage : certains auteurs ont utilisé les nouvelles technologies, par exemple l’IPad, pour enseigner la numératie, par exemple la numératie fonctionnelle avec d’autres publics (Burton et coll., 2013), on ne dispose toutefois pas de recul sur les apports de ce type de mesure avec le public ayant une DI.

Cette deuxième famille d’approches s’appuie sur les modèles développés en psychologie cognitive et/ou dans le champ des neurosciences (Kearns et Fuchs, 2013). L’objectif est d’agir de façon ciblée sur les fondements cognitifs de la compréhension numérique en prenant en compte les spécificités du fonctionnement cognitif de l’apprenant. Celles-ci servent à orienter l’intervention. Les habiletés ciblées sont les processus qui servent de socle à la construction des compétences numériques ultérieures (subitizing, estimation, ligne numérique, représentation symbolique). Le choix des habiletés sur lesquelles porte l’intervention procède d’une évaluation cognitive et/ou neuropsychologique complète et personnalisée. Cette approche postule que : « les difficultés arithmétiques peuvent être considérablement réduites par l’intervention, spécialement les interventions basées sur les modèles qui appréhendent l’arithmétique comme organisée en plusieurs sous-composantes et les interventions qui prennent en compte les forces et les faiblesses spécifiques des individus » (Dowker, 2005, p. 4, traduction libre).

L’intervention ciblée sur les processus spécifiques vise à entraîner et/ou à optimiser les processus déficitaires. « En principe, la correspondance entre le déficit et l’instruction est l’essence de l’instruction cognitive ciblée » (Kearns et Fuchs, 2013, p. 265). Ce type d’intervention peut être dispensé en groupe, en individuel ou de façon assistée par ordinateur25 . Actuellement, cette intervention ciblée est surtout introduite auprès d’enfants typiques aux prises avec une dyscalculie sévère et sous la forme d’une remédiation (Cohen Kadosh et coll., 2013). En France, l’Unité Inserm-CEA de neuro-imagerie cognitive a développé deux logiciels gratuits de jeux mathématiques disponibles en français et destinés aux enfants tout-venant jusqu’à 10 ans. Ces programmes permettent notamment d’entraîner les bases de la connaissance du nombre et de l’arithmétique26 , par exemple l’estimation numérique, le comptage, les calculs élémentaires (additions et soustractions) ou encore les systèmes de notation. On sait, grâce aux observations menées dans la population typique adulte, que l’enseignement des mathématiques dispensé à l’âge scolaire contribue à perfectionner les habiletés d’estimation assurées par le système d’approximation dont chacun hérite en principe dans son bagage phylogénétique. Cette amélioration concerne aussi les adultes qui deviennent plus rapides et plus précis dans des tâches d’estimation de numérosité après entraînement (Nys et coll., 2013).

L’introduction de programmes similaires auprès des personnes ayant une DI débute à peine. En France, Vilette et Meyer (2014) évaluent l’effet de l’introduction d’un entraînement de mise en correspondance entre les connaissances numériques symboliques et les représentations analogiques chez des enfants avec une T21 (âgés de 9 à 14 ans). L’entraînement comprend 6 séances. Il est réalisé à l’aide d’un logiciel (l’Estimateur) spécialement développé dans le but d’entraîner les enfants à coordonner les représentations numériques symboliques et les représentations analogiques. Dans cette étude, l’entraînement visait à soutenir le traitement analogique à l’aide des processus symboliques. Les résultats de cette étude ne sont pas encore disponibles.

Les approches cognitives incarnées s’inscrivent dans une perspective théorique qui prend le contrepied de la conception cognitiviste précédente. Elles découlent des théories de la cognition incarnée qui considèrent que les fonctions cognitives supérieures tirent leurs racines de l’activité et de l’expérience corporelle (et sensorielle). Ainsi, le développement du concept de nombre ne résulterait pas du seul fonctionnement cognitif, mais nécessiterait, pour son émergence, que l’apprenant en fasse l’expérience au cours de ses interactions avec l’environnement. Cette perspective théorique ouvre sur de nouvelles formes d’interventions. L’action consiste à proposer à l’apprenant de faire des expériences corporelles en lien avec le concept enseigné (Fischer et coll., 2011). C’est pourquoi, dans une étude randomisée, Link et coll. (2013) ont entraîné la compréhension de la ligne numérique et l’estimation de valeurs numériques jusqu’à 100 en proposant à des élèves de 7 ans de se déplacer physiquement sur une ligne. Leurs résultats montrent que le groupe d’enfants progresse significativement en comparaison du groupe témoin. L’apport de ce type d’intervention, tout juste introduit auprès des enfants typiques, n’a pour l’instant pas été documenté pour le public ayant une déficience intellectuelle.

Les approches indirectes tentent d’améliorer les compétences numériques en agissant sur des fonctions supportant le traitement du nombre sans lui être exclusivement dévolues.

L’approche métacognitive (ou enseignement stratégique) vise à aider l’apprenant à prendre conscience de son propre fonctionnement cognitif. Elle repose sur le postulat selon lequel l’entraînement des habiletés métacognitives permet d’améliorer le niveau de métacognition qui, à son tour, peut permettre une amélioration des habiletés scolaires. L’approche pédagogique incite l’élève à construire des connaissances explicites concernant son propre fonctionnement cognitif et lui apprend ensuite à les utiliser pour contrôler et adapter intentionnellement son fonctionnement en vue d’atteindre un objectif d’apprentissage (Romainville, 2007).

« Au cours de l’intervention, l’élève apprend à repérer les aspects pertinents de la tâche, évaluer le besoin d’une approche stratégique, à adapter la stratégie à son propre fonctionnement et à la spécificité de la tâche, à contrôler le fonctionnement de la stratégie et la qualité de la performance ainsi qu’à comparer consciemment la situation présente à d’autres situations connues » (Büchel et Paour, 2005, p. 228).

L’intervention a un objectif stratégique, dans le sens où elle suppose une transmission systématique des outils du fonctionnement intellectuel dans le but de « permettre à un individu de remédier à ses processus déficitaires par l’acquisition de stratégies cognitives » (Büchel et Paour, 2005, p. 228-229). En termes de bénéfices, l’approche métacognitive estime pouvoir favoriser la construction et l’utilisation indépendante de stratégies d’apprentissages chez les apprenants. Son action est voisine de l’« apprentissage autorégulé » (Pintrich et Zeidner, 2000) et se superpose à l’« auto-instruction » (Wilson et Räsänen, 2009 ; voir de Boer et coll., 2012 ou Dinsmore et coll., 2008 pour une discussion détaillée entre ces concepts).

Plusieurs travaux de synthèse ou méta-analyses successives confirment que l’approche métacognitive a des effets modérés voire importants sur l’apprentissage scolaire des élèves typiques (Hattie et coll., 1996 ; Dignath et Büttner, 2008 ; Dignath et coll., 2008). La recherche fournit aussi certaines précisions sur l’efficacité différentielle de ce type d’intervention selon le public-cible, les matières enseignées, l’auteur, la durée et la stratégie d’intervention utilisée. Après avoir analysé 74 études publiées entre 1992 et 2006, Dignath et Büttner (2008) rapportent par exemple que les effets de l’approche métacognitive sur les performances des élèves de CE et CM sont deux fois plus importants en mathématiques (Cohen’s d = 0,96 ; SE = 0,13) qu’en lecture ou écriture (Cohen’s d = 0,44 ; SE = 0,006). En revanche, au niveau secondaire, la métacognition a des effets plus marqués en lecture et en écriture (Cohen’s d = 0,92 ; SE = 0,20) qu’en mathématiques (Cohen’s d = 0,96 ; SE = 0,08). Cette analyse porte à conclure qu’en ce qui concerne les mathématiques, l’approche métacognitive est plus efficace en primaire.

De Boer et coll. (2012) ont analysé des études publiées entre 2000 et 2011, concernant les élèves entre 5 et 17 ans, élèves avec besoins éducatifs particuliers inclus, et répondant aux critères de pratiques fondées sur les preuves (Evidence based practices), soit au total, 95 études. Sur ces 95 interventions rapportées dans 58 articles, 44 portaient sur les mathématiques, 23 sur la compréhension en lecture, 16 sur l’écriture d’un texte, 9 en sciences et 3 sur d’autres sujets. Leurs résultats témoignent d’un effet massif de ce type d’intervention sur l’écriture de texte, et d’effets modérés à importants sur les performances en mathématiques et en sciences. Dans ces disciplines, les résultats montrent que la plupart des élèves bénéficiant d’une intervention métacognitive améliorent leurs performances scolaires. Les résultats indiquent aussi que les élèves avec des besoins éducatifs particuliers tirent légèrement plus de profit de cette forme d’instruction que leurs pairs typiques (estimation de la différence de la taille de l’effet = 0,23 ; SE = 0,12 ; p = 0,058). L’intervention métacognitive est profitable aux élèves quel que soit leur niveau scolaire. Les habiletés doivent être explicitement enseignées car la plupart des apprenants n’ont pas spontanément conscience de leurs forces et de leurs faiblesses, et/ou ne parviennent pas à les développer à travers leurs expériences mathématiques (Desoete et coll., 2003).

Dignath et Büttner (2008) rapportent que les interventions courtes (±10 semaines) se révèlent tout aussi efficaces, si ce n’est plus, que les interventions longues (±20 semaines). Classées par ordre décroissant, les stratégies métacognitives les plus fréquemment enseignées en lien avec les mathématiques sont : le monitoring (contrôle), la planification (prédiction), l’évaluation (réflexion) et la stratégie dite d’élaboration. Significativement plus efficace que les autres, cette dernière suppose d’apprendre à l’élève à faire explicitement appel à ses connaissances antérieures, à faire activement des liens entre les nouvelles connaissances et celles déjà construites afin de faciliter la consolidation de l’apprentissage et le passage en mémoire à long terme. Les auteurs concluent qu’en ce qui concerne les mathématiques, l’enseignement stratégique devrait au moins porter sur la stratégie dite d’élaboration (Dignath et Büttner, 2008). En ce qui concerne les personnes avec une DI, la métacognition est considérée comme un « construct important » pour la compréhension de la DI (Saldaña, 2004). La prise en considération de la métacognition dans la planification de l’éducation, notamment de l’éducation mathématique, des personnes avec une DI reste cependant encore rare et peu documentée.

Nous avons pris le parti de distinguer la remédiation cognitive de l’approche métacognitive. Veenman et coll. (2006) rappellent en effet que les deux approches ne sont pas totalement superposables. La remédiation cognitive vise à renforcer et/ou à optimiser le fonctionnement des processus cognitifs généraux (Kearns et Fuchs, 2013) alors que la métacognition, comme décrit plus haut, a pour but d’aider l’apprenant à prendre conscience de son propre fonctionnement cognitif. Il est toutefois vrai que « la métacognition puise dans la cognition » et qu’« en ce qui concerne les habiletés métacognitives, un individu ne peut pas s’engager dans la planification sans mener des activités cognitives » (Veenman et coll., 2006, p. 5).

L’approche de remédiation cognitive considère que les difficultés de compréhension du nombre résultent de limitations présentes dans les processus cognitifs généraux (cf. tableau 11.I). Le postulat sous-jacent consiste à affirmer que l’entraînement de fonctions cognitives comme par exemple mémoire de travail, attention, raisonnement, fonctions exécutives, langage, etc., n’améliorera pas seulement l’aptitude sur laquelle porte l’entraînement, mais que les progrès réalisés pourront se transférer à des tâches autres que celles exercées, et ceci pour le plus grand intérêt de la personne concernée (voir Perrig et coll., 2009 pour une revue). Au niveau de l’intervention, deux variantes sont présentes : l’approche cognitive peut être délivrée seule ou en combinaison avec l’enseignement de contenus académiques ou adaptatifs (Kearns et Fuchs, 2013 ; Carteau-Martin et coll., 2014). Kearns et Fuchs (2013) font cependant remarquer que les pratiques en la matière sont sujettes à des recommandations diverses sans qu’un état systématique de la recherche n’ait été réalisé.

C’est pour cette raison que ces deux chercheurs ont procédé, en 2013, à une revue compréhensive systématique des interventions cognitives destinées à améliorer les compétences académiques des élèves avec troubles spécifiques de l’apprentissage, efficience adaptative ou intellectuelle subnormale (± 1 écart-type) ou ayant un « faible rendement scolaire ». Cette étude visait à vérifier si les interventions cognitives soutenaient plus efficacement les performances scolaires lorsqu’elles étaient paramétrées pour répondre de façon personnalisée aux besoins et aux limitations cognitives de l’élève. La plus-value de ce type d’intervention par rapport aux approches pédagogiques classiques était aussi questionnée. Seules les études expérimentales et quasi-expérimentales ont été retenues dans cette analyse qui a couvert les publications parues en anglais depuis 1988. Les auteurs ont identifié 50 études (pour 39 articles) répondant à leurs critères d’inclusion. Dans 13 études sur 50, l’intervention concernait des personnes avec une efficience intellectuelle subnormale contre 21 avec un trouble spécifique et 16 un « faible rendement scolaire ». Cette synthèse montre qu’à l’heure actuelle les élèves ayant des difficultés en lecture ou en écriture sont les principaux destinataires des approches de remédiation cognitive. Seuls six articles portaient sur l’impact de telles interventions sur les habiletés numériques des élèves. Au terme de leur analyse, les auteurs rapportent que sur 11 études ayant tenté de comparer les bénéfices de la remédiation cognitive à ceux d’une intervention pédagogique classique, seules 2 rapportent des effets significatifs en faveur de l’intervention cognitive, 5 font état de gains d’apprentissage comparables entre les deux approches, 1 étude conclut à une efficacité supérieure de l’intervention pédagogique classique alors que 3 ne permettent pas de vraie comparaison. Ces résultats les portent à conclure au fait que les mesures de remédiation, bien que possiblement prometteuses, en sont encore à leurs premiers balbutiements, et que les recommander serait actuellement prématuré. Cette analyse, même si elle reste en demi-teinte du fait du peu d’études de qualité, n’a pas d’équivalent dans le champ de la DI. Un point de situation analogue serait pourtant nécessaire étant donné que des mesures de remédiation cognitive sont régulièrement proposées aux personnes concernées (par exemple Frenkel et Bourdin, 2009).

La dernière famille d’intervention consiste à aménager l’environnement. Le but est de faciliter et d’optimiser la manière dont l’apprenant traite les informations numériques en adaptant les tâches pour que celles-ci deviennent accessibles et en s’appuyant sur les différentes manières de présenter et représenter les signaux. Ces aménagements répondent au principe de « conception universelle27  » dont l’objectif est de rendre les milieux et les informations « accessibles, compréhensibles et utilisables par tous […] » (Ginnerup, 2009, p. 8).

L’aménagement de l’environnement intervient comme une prothèse cognitive. L’intervention consiste, par exemple, à autoriser une calculette afin de ne pas solliciter excessivement les ressources mentales de l’apprenant (encodage, traitement de l’information, charge mentale) ou à choisir un indiçage numérique facilitant l’évocation des nombres et convenant à l’apprenant. Dans une méta-analyse, Gersten et coll. (2009) identifient 13 études randomisées ayant impliqué des participants entre 6 et 14 ans en situation de handicap mais sans indication diagnostique précise. Ces études ont évalué le rôle joué par la présentation des données sur les performances des élèves. Leurs résultats permettent d’affirmer que la présentation des nombres sous une forme concrète et manipulable ainsi que sous une forme figurative (diagramme, dessin, pictogramme, etc.) améliore les performances générales en mathématiques, les concepts de pré-algèbre, les situations-problèmes et les opérations.

De leur côté, Hord et Bouck (2012) rapportent l’efficacité tendancielle de l’introduction de supports imagés et de fiches, pour soutenir l’apprentissage des faits mathématiques à des élèves d’âge scolaire ayant une DI légère. Les aménagements se sont avérés bénéfiques pour la mémorisation des tables de multiplication (Sante et coll., 2001 ; Hayter et coll., 2007 ; Rao et Mallow, 2009 ; Hord et Bouck, 2012). En raison de caractéristiques individuelles dans la manière de traiter les informations, certains formats de présentation des données s’avèrent plus ou moins adaptés aux besoins de l’apprenant (Booth et Koedinger, 2012). Dans le champ de la DI, on sait que les personnes avec une T21 décodent mieux les informations numériques lorsqu’elles sont présentées visuellement (Fidler et coll., 2006 ; Fidler et Nadel, 2007). C’est dans cette même perspective que s’inscrivent les interventions jouant sur les conditions de présentation multi- ou mono-sensorielle des informations. À ce jour, les avantages d’un mode de présentation par rapport à l’autre n’ont été étudiés que dans la population tout-venant. Jordan et Baker (2011) rapportent à ce propos que les enfants typiques entre 3 et 5 ans font preuve de plus d’exactitude dans des tâches de discrimination lorsque les quantités à estimer ou à comparer leur sont proposées dans un format multisensoriel (son + image) versus dans un format mono-sensoriel (son ou image seulement). Ces résultats accréditent la thèse dite de « redondance intersensorielle » selon laquelle le traitement d’une information est facilité par une présentation multimodale de l’information comparativement à une présentation unimodale (Shams et Seitz, 2008).

Malgré des preuves encore peu nombreuses, l’ergonomie cognitive semble prometteuse, les parents, les enseignants et les autres professionnels, doivent être encouragés à rendre accessibles les tâches et à utiliser un indiçage alternatif, par exemple, en jouant sur les différentes manières de représenter graphiquement ou numériquement les quantités pour faciliter le calcul, les algorithmes, le comptage/dénombrement, la production de la « comptine numérique » ou encore la résolution de problèmes.

L’efficacité de l’intervention est aussi en lien avec la motivation de l’apprenant. Or, la cognition académique est une « cognition froide » (Brown et coll., 1983). Une centration exclusive sur des connaissances et des stratégies purement cognitives n’est actuellement plus acceptable et risque d’interférer avec l’efficacité de l’intervention (Dai et Sternberg, 2004 ; de Corte, 2010 ; Berger et Büchel, 2012). La plupart des interventions n’intègrent pas la dimension motivationnelle hormis les interventions situées dans lesquelles elle est présente de façon implicite. Les interventions métacognitives dont l’action s’étend en principe à la motivation présentent la même faiblesse lorsqu’elles visent l’apprentissage des mathématiques. De Boer et coll. (2012) rapportent que parmi les 44 interventions métacognitives portant sur la numératie, seulement dix interventions mettent l’accent sur les stratégies motivationnelles. Sept proposent des stratégies en lien avec le sentiment d’auto-efficacité en numératie des apprenants, trois explorent leurs buts et leurs attentes vis-à-vis du contenu enseigné, aucune ne se penche sur la pertinence qu’ils accordent ou non à ce type de savoir. Le calcul de la taille de l’effet se heurtant au peu d’études disponibles, les auteurs n’ont pu calculer la taille de l’effet que pour les interventions ayant tenté d’agir sur le sentiment d’auto-efficacité. En l’état de la recherche, leurs résultats ne confirment pas l’effet de ce type d’intervention sur les performances en numératie.

L’accent mis sur la motivation à l’apprentissage est plus soutenu dans les interventions portant sur l’écriture. En revanche, l’enseignement de la lecture ignore presque complètement cette question.

Le rôle de la motivation sur les apprentissages scolaires de base et le soutien pouvant être accordé à cette dimension, demandent à être investigués de façon plus systématique. Wendling et Mather (2009) rapportent qu’une majorité d’enfants typiques jugent les mathématiques « plus difficiles » que la lecture. Les personnes avec une DI expriment moins de plaisir à l’apprentissage des mathématiques qu’à celui de la lecture ou de l’écriture. Petitpierre et coll. (2013) ont abordé le thème des apprentissages tout au long de la vie chez 60 personnes avec une DI légère, parmi lesquelles 24 avec une T21. Les personnes interrogées, âgés de 18 à 73 ans, disent surtout mobiliser les connaissances mathématiques dans des tâches domestiques (par exemple, faire un budget, leurs paiements, vérifier le retour de monnaie lors d’un achat ou encore mettre la table pour le bon nombre de personnes) et dans le cadre de leurs activités professionnelles. Certaines disent aussi en faire usage dans leurs loisirs (par exemple lors de participation au loto, ou pour la comparaison des résultats sportifs). Les mathématiques leur sont également nécessaires pour l’utilisation des ressources communautaires, comme par exemple prendre son ticket de bus à l’automate (choix de la zone, paiement du ticket). L’intensité à laquelle les personnes interviewées disent mobiliser les mathématiques à l’âge adulte n’est pas dépendante de la manière dont elles disent avoir apprécié cet apprentissage à l’âge scolaire. En revanche, on note une relation significative entre la manière dont elles disent avoir apprécié les apprentissages effectués à l’école (modalité dichotomique j’ai aimé/je n’ai pas aimé) et l’expression de leurs projets d’apprentissage actuels (Petitpierre et coll., 2013).

Les manuels traitant de l’éducation des élèves avec une DI n’abordent que rarement l’enseignement des mathématiques. Du côté de la recherche, on constate un manque d’études permettant de guider l’intervention dans le domaine (Browder et coll., 2012). La tâche consistant à identifier des formes d’interventions efficaces à l’intention des personnes avec une DI est compliquée par de multiples facteurs. Les tentatives de synthèse se heurtent à la qualité des études et à l’atomisation de la littérature. Les études disponibles sont difficiles à rapprocher et à comparer du fait de la diversité des conditions d’administration et de mise en œuvre des interventions, ainsi qu’en raison de la diversité et de l’hétérogénéité du public concerné (Odom et coll., 2005 ; Montgomery, 2006).

Les connaissances actuelles en matière d’instruction des mathématiques chez les personnes avec une DI sont donc parcellaires. Toutefois quelques constats peuvent être dégagés.

En ce qui concerne les modalités d’enseignement, l’instruction structurée et l’enseignement situé sont les manières les plus fréquemment utilisées pour enseigner la numératie aux personnes ayant une DI (Browder et coll., 2008 ; Hord et Bouck, 2012). L’efficacité de l’instruction structurée est confirmée par plusieurs études de bonne qualité, toutefois cette approche ne convient pas à tous les apprenants (Browder et coll., 2008 ; Gersten et coll., 2009 ; Vaughn et coll., 2012). L’instruction en contexte réel est profitable (Xin et coll., 2005 ; Browder et coll., 2008). Bien que l’on sache l’approche constructiviste bénéfique à la population typique notamment pour ce qui est de l’apprentissage du sens du nombre et des connaissances préscolaires (Wilson et Räsänen, 2009), le manque de littérature ne permet pas de se prononcer sur son efficacité auprès des personnes avec une DI. Concernant les interventions indirectes, la prise en considération de la métacognition dans l’éducation mathématique des personnes avec une DI est rare et peu documentée et ses effets – modérés à importants sur les mathématiques – s’infèrent des études portant sur une population plus large avec des besoins éducatifs particuliers (Desoete et coll., 2003 ; De Boer et coll., 2012). Les sciences cognitives et les neurosciences proposent désormais des théories sur la compréhension de la cognition mathématique, ainsi qu’un ensemble d’outils basés sur ces nouveaux modèles et pouvant contribuer à élargir les moyens d’action auprès du public avec une DI (De Smedt et coll., 2011). L’application de ces programmes auprès du public avec une DI débute. Le défi des années à venir consistera à en tester systématiquement l’usage et à en vérifier la plus-value, pour les personnes concernées.

En ce qui concerne les contenus enseignés, peu d’interventions travaillent la compréhension et le sens du nombre. L’apprentissage procédural, c’est-à-dire l’entraînement de séquences d’actions permettant de résoudre un problème académique (calcul, opérations élémentaires, etc.) ou fonctionnel (manipulation de l’argent, etc.), constitue l’objectif d’enseignement le plus fréquent. L’apprentissage procédural est important car il est à l’origine de l’automaticité qui permet d’accroître la vitesse et l’exactitude des réponses lors de la résolution d’opérations (Dehn, 2008 ; Thevenot et Masson, 2013). Malgré leur rôle capital, le sens du nombre, le raisonnement mathématique et les connexions concret-abstrait sont des contenus négligés actuellement, il est indispensable qu’ils soient entraînés de façon plus systématique (Hord et Bouck, 2012). La littérature rapporte que les personnes avec une DI sont rarement encouragées à développer des savoirs plus exigeants que les opérations et les connaissances de base, ce qui peut les désavantager pour leur insertion dans la communauté (Browder et coll., 2008 et 2012).

Plusieurs questions restent actuellement ouvertes sur la meilleure manière d’enseigner les contenus mathématiques (Thevenot et Masson, 2013). Il apparaît urgent de faire de l’étude de l’efficacité des interventions en mathématiques, une priorité de la recherche dans le domaine des apprentissages scolaires. Pour ce public, comme pour la population typique, l’attractivité de l’apprentissage des mathématiques est faible et souvent anxiogène. Pourtant les aspects motivationnels sont rarement stimulés (Petitpierre et coll., 2014).

En conclusion, la recherche a permis de produire des connaissances scientifiques considérables qui permettent de mieux comprendre le fonctionnement de la cognition numérique. Ces connaissances permettent d’éclairer les difficultés, mais aussi les ressources, qui s’extériorisent lorsque les personnes avec une DI sont confrontées aux apprentissages mathématiques ou à des tâches du quotidien qui font appel au nombre.

Compte tenu du fait que les habiletés numériques constituent une composante forte à l’adaptation et à la participation sociale, mieux comprendre le fonctionnement de ce public et être capables de lui offrir des soutiens et des aménagements pédagogiques ciblés et adaptés s’avère primordial (Price et coll., 2013).

[1] albus d, thurlow m. 2010-11 publicly reported assessment results for students with disabilities and ells with disabilities (technical report 68). University of Minnesota, National Center on Educational Outcomes; 2013;

[2] ansari d, donlan c, thomas ms, ewing sa, peen t, karmiloff-smith a. What makes counting count ? Verbal and visuo-spatial contributions to typical and atypical number development. J Exp Child Psychol. 2003; 85:50-62

[3] ansari d, donlan c, karmiloffsmith a. Typical and atypical development of visual estimation abilities. Cortex. 2007; 43:758-768

[4] antshel km, fremont w, kates wr. The neurocognitive phenotype in velo-cardiofacial-syndrome : a developmental perspective. Dev Disabil Res Rev. 2008; 14:43-51

[5] barrouillet p, bernardin s, portrat s, vergauwe e, camos v. Time and cognitive load in working memory. J Exp Psychol Learn Mem Cogn. 2007; 33:570-585

[6] barrouillet p, gavens n, vergauwe e, gaillard v, camos v. Working memory span development : a time-based resource-sharing model account. Dev Psychol. 2009; 45:477-490

[7] beadle-brown j, murphy g, wing l, gould j, shah a, et coll. . Changes in skills for people with intellectual disability : a follow-up of the Camberwell Cohort. J Intellect Disabil Res. 2000; 44:12-24

[8] bellugi u, lichtenberger l, jones w, lai z, georges m. The neurocognitive profile of Williams syndrome : a complex pattern of strenghts and weaknesses. J Cogn Neurosci. 2000; 12:7-29

[9] berger jl, büchel f. Métacognition et croyances motivationnelles : un mariage de raison. Revue Française de Pédagogie. 2012; 179:95-128

[10] bonato m, zorzi m, umiltã c. When time is space : Evidence for a mental time line and for a common magnitude system. Neurosci Biobehav Rev. 2012; 36:2257-2273

[11] booth jl, koedinger kr. Are diagrams always helpful tools ? Developmental and individual differences in the effect of presentation format on student problem solving. Br J Educ Psychol. 2012; 82:492-511

[12] briars dj, siegler rs. A featural analysis of preschoolers’ counting knowledge. Dev Psychol. 1984; 20:607-618

[13] brigstocke s, hulme c, nye j. Number and arithmetic skills in children with Down syndrome. Downs Syndr Res Pract. 2008; 74-77

[14] browder dm, spooner f, ahlgrim-delzell l, harris aa, wakeman sy. A meta-analysis on teaching mathematics to students with significant cognitive disabilities. Exceptional Children. 2008; 74:407-432

[15] browder dm, jimenez ba, trela k. Grade-aligned math instruction for secondary students with moderate intellectual disability. Education Training Autism Dev Disabil. 2012; 47:373-388

[16] brown al, bransford jd, ferrara ra, campione jc. Learning, remembering, and understanding. In: mussenph, flavelljh, markmanem, editors. Handbook of child psychology. New York:Wiley; 1983. p. 77-166

[17] büchel f, paour jl. Déficience intellectuelle : déficits et remédiation cognitive. Enfance. 2005; 3:227-240

[18] bull r. Neuropsychological factors. In: berchdb, mazzoccommm, editors. Why is math so hard for some children ? The nature and origins of mathematics learning difficulties and disabilities. Baltimore:Paul H. Brookes; 2007. p. 265-227

[19] burton ce, anderson dh, prater ma, dyches tt. Video self-modeling on an iPad to teach functional math skills to adolescents with autism and intellectual disability. Focus Autism Dev Disabil. 2013; 28:67-77

[20] butterworth b. The Mathematical Brain. London:Macmillan; 1999.

[21] butterworth b. Foundational numerical capacities and the origins of dyscalculia. Trends Cogn Sci. 2010; 14:534-541

[22] camos v. Numerosity discrimination in children with Down syndrome. Dev Neuropsychol. 2009; 34:435-447

[23] camos v, barrouillet p. Le développement de la mémoire de travail : perspectives dans le cadre du modèle de partage temporel des ressources. Psychologie Française. 2013; 59:21-39

[24] camp js, farran e, karmiloff-smith a. Numeracy. In: farrane, karmiloff-smitha, editors. Neurodevelopmental disorders across the lifespan : the neuroconstructivist approach. Oxford:Oxford University Press; 2011. p.

[25] campbell jid. Architecture for numerical cognition. Cognition. 1994; 53:1-44

[26] campbell le, azuma r, ambery f, stevens a, smith a, et coll. . Executive functions and memory abilities in children with 22q11.2 deletion syndrome. Austr NZ J Psychiatry. 2010; 44:364-371

[27] carey s. The Origin of Concepts. New York:Oxford University Press; 2009.

[28] carrasumada s, vendrell r, ribera g, montserrat m. Cognitive processes related to counting in students with special educational needs. Eur J Spec Needs Educ. 2006; 21:135-150

[29] carteau-martin i, amado i, thillay a, houy-durand e, barthelemy c, et coll. . Aspects théoriques et pratiques de la remédiation cognitive dans la déficience intellectuelle du jeune adulte : la « cognitive remediation therapy » (CRT) peut-elle être adaptée ?. L’Encéphale. 2014; (Doi :10.1016/j.encep.2014.02.004)

[30] caycho l, gunn p, siegal m. Counting by children with Down Syndrome. Am J Ment Retard. 1991; 95:575-583

[31] cohen kadosh r, dowker a, heine a, kaufmann l, kucian k. Interventions for improving numerical abilities : Present and future. Trends Neurosci Educ. 2013; 2:85-93

[32] cornish k, scerif g, karmiloff-smith a. Tracing syndrome-specific trajectories of attention across the lifespan. Cortex. 2007; 43:672-685

[33] cote d. Implementing a problem-solving intervention with students with mild to moderate disabilities. Interv Sch Clin. 2011; 46:259-265

[34] dai dy, sternberg rj. Beyond cognitivism : Toward an integrated understanding of intellectual functioning and development. In: daidy, sternbergrj, editors. Motivation, emotion, and cognition : integrative perspectives on intellectual functioning and development. Mahwah:Lawrence Erlbaum; 2004. p. 3-38

[35] davies m, howlin p, udwin o. Independence and adaptive behaviour in adults with Williams syndrome. Am J Med Genet. 1997; 70:188-195

[36] de boer h, donker-bergstra a, kostons d. Effective strategies for self-regulated learning : a meta-analysis. Rijksuniversiteit Groningen: The Netherlands. GION : Gronings Instituut voor Onderzoek van Onderwijs; 2012;

[37] de clercq a, desoete a, roeyers h. EPA 2000 : a multilingual, programmable computer assessment of off-line metacognition in children with mathematical-learning disabilities. Behav Res Methods Instrum Comput. 2000; 32:304-311

[38] de corte e. Historical developments in the understanding of learning. In: dumonth, istanced, benavidesf, editors. The nature of learning. Using research to inspire practice. Paris:OCDE; 2010. p. 35-67

[39] de corte e, greer b, verschaffel l. Mathematics teaching and learning. In: berlinerdc, calfeerc, editors. Handbook of educational psychology. New York:Macmillan; 1996. p. 491-549

[40] de smedt b, swillen a, devriendt k, fryns jp, verschaffel l, et coll. . Mathematical disabilities in young primary school children with velo-cardio-facial syndrome. Genet Couns. 2006; 17:259-280

[41] de smedt b, swillen a, devriendt k, fryns jp, verschaffel l, et coll. . Mathematical disabilities in children with velo-cardio-facial syndrome. Neuropsychologia. 2007; 45:885-895

[42] de smedt b, swillen a, devrient k, fryns jp, verschaffel l, et coll. . Cognitive correlates of mathematical disabilities in children with velo-cardio-facial syndrome. Genet Couns. 2008; 19:71-94

[43] de smedt b, swillen a, verschaffel l, ghesquiere p. Mathematical learning disabilities in children with 22q11.2 deletion syndrome : a review. Dev Disabil Res Rev. 2009; 15:4-10

[44] de smedt b, ansari d, grabner rh, hannula-sormunen m, schneider m, et coll. . Cognitive neuroscience meets mathematics education : It takes two to Tango. Educ Res Rev. 2011; 6:232-237

[45] dehaene s. Varieties of numerical abilities. Cognition. 1992; 44:1-42

[46] dehaene s. The number sense : how the mind creates mathematics. New York:Oxford University Press; 1997.

[47] dehaene s. La bosse des maths (édition revue et augmentée). Paris:Odile Jacob; 2010.

[48] dehaene s. The number sense : how the mind creates mathematics (revised and updated edition). New York:Oxford University Press; 2011.

[49] dehaene s, cohen l. Towards an anatomical and functional model of number processing. Mathematical Cognition. 1995; 1:83-120

[50] dehaene s, dupoux e, mehler j. Is numerical comparison digital ? Analogical and symbolic effects in two-digit number comparison. J Exp Psychol Hum Percept Perform. 1990; 16:626-641

[51] dehaene s, dehaene-lambertz g, cohen l. Abstract representations of numbers in the animal and human brain. Trends Neurosci. 1998; 21:355-361

[52] dehaene s, spelke e, pinel p, stanescu r, tsivkin s. Sources of mathematical thinking : Behavioral and brain-imaging evidence. Science. 1999; 284:970-974

[53] dehaene s, piazza m, pinel p, cohen l. Three parietal circuits for number processing. Cogn Neuropsychol. 2003; 20:487-506

[54] dehn mj. Working Memory and academic learning : assessment and intervention. Hoboken, NJ:John Wiley & Sons, Inc.; 2008.

[55] desoete a, roeyers h, de clercq a. Can off-line metacognition enhance mathematical problem solving ?. J Educ Psychol. 2003; 95:188-200

[56] dignath c, büttner g. Components of fostering self-regulated learning among students. A meta-analysis on intervention studies at primary and secondary school level. Metacognition Learning. 2008; 3:231-264

[57] dignath c, büttner g, langfeldt h. How can primary school students learn selfregulated learning strategies most effectively ? A meta-analysis on self-regulation training programmes. Educ Res Rev. 2008; 3:101-129

[58] dinsmore dl, alexander pa, loughlin sm. Focusing the conceptual lens on metacognition, self-regulation, and self-regulated learning. Educ Psychol Rev. 2008; 20:391-409

[59] donlan c. Le rôle du langage dans le développement des mathématiques : voies typiques et atypiques. Réseau Canadien de Recherche sur le Langage et l’Alphabétisation. 2009;

[60] dowker a. Individual differences in arithmetical abilities. Implications for psychology, neurosciences and education. Hove:Psychology Press; 2005.

[61] dykens em, hodapp rm, finucane b. Genetics and Mental Retardation Syndromes : A New Look at Behavior and Intervention. Baltimore:Brookes; 2000.

[62] eliez s, blasey cm, menon v, white cd, schmitt e, et coll. . Functional brain imaging study of mathematical reasoning abilities in velocardiofacial syndrome (del22q11.2). Genet Med. 2001; 3:49-55

[63] faragher r, brown ri. Numeracy for adults with Down syndrome : it’s a matter of quality of life. J Intellect Disabil Res. 2005; 49:761-765

[64] faragher r, clarke b. Educating learners with Down syndrome : research, theory, and practice with children and adolescent. Abingdon:Routledge; 2014.

[65] farran k, karmiloff-smith a. Neurodevelopmental disorders across the lifespan : a neuroconstructivist approach. Oxford:Oxford University Press; 2012.

[66] feigenson l, dehaene s, spelke e. Core systems of number. Trends cogn Sci. 2004; 8:307-314

[67] fidler dj, nadel l. Educating children with Down syndrome : neuroscience, development, and intervention. Ment Retard Dev Disabil Res Rev. 2007; 13:262-271

[68] fidler dj, hepburn s, rogers s. Early learning and adaptive behaviour in toddlers with Down syndrome : Evidence for an emerging behavioural phenotype ?. Downs Syndr Res Pract. 2006; 9:37-44

[69] fischer u, moeller k, bientzle m, cress u, nuerk hc. Sensori-motor spatial training of number magnitude representation. Psychon Bull Rev. 2011; 18:177-183

[70] foegen a. Algebra progress monitoring and Interventions for students with learning disabilities. Learn Disabil Q. 2008; 31:65-78

[71] forster s. Age-appropriateness : enabler or barrier to a good life for people with profound intellectual and multiple disabilities ?. J Intellect Dev Disabil. 2010; 35:129-131

[72] frenkel s, bourdin b. Verbal, visual, and spatio-sequential short-term memory : assessment of the storage capacities of children and teenagers with Down’s syndrome. J Intellect Disabil Res. 2009; 53:152-160

[73] frye d, baroody aj, burchinal m, carver sm, jordan nc, et coll. . Teaching math to young children : a practice guide (NCEE 2014-4005). National Center for Education Evaluation and Regional Assistance (NCEE), Institute of Education Sciences, Department of Education; 2013.

[74] gaillard f. NUMERICAL. Test neurocognitif pour l’apprentissage du nombre et du calcul. Lausanne:Université de Lausanne; 2000.

[75] gelman r, cohen m. Qualitative differences in the way Down syndrome and normal children solve a novel counting problem. In: nadell, editors. The psychobiology of Down’s syndrome. Cambridge, MA:MIT Press; 1998. p. 51-99

[76] gelman r, gallistel cr. The child’s understanding of number. Cambridge, Mass:Harvard University Press; 1978.

[77] gersten r, beckmann s, clarke b, foegen a, marsh l, et coll. . Assisting students struggling with mathematics : response to intervention (rti) for elementary and middle schools (NCEE 2009-4060). National Center for Education Evaluation and Regional Assistance, Institute of Education Sciences, US Department of Education; 2009.

[78] giesen jm, cavenaugh bs, mcdonnall mc. Academic supports, cognitive disability and mathematics achievement for visually impaired youth : a multilevel modeling approach. Int J Spec Educ. 2012; 27:17-26

[79] ginnerup ms. Assurer la pleine participation grâce à la conception universelle. Conseil de l’Europe; 2009.

[80] glidden lm, schoolcraft sa. From diagnosis to adaptation : Optimizing family and child functioning when a genetic diagnosis is associated with mental retardation. In: mazzoccommm, rossjl, editors. Neurogenetic developmental disorders : manifestation and identification in childhood. Cambridge:The MIT Press; 2007. p. 391-413

[81] halberda j, mazzocco mmm, feigenson l. Individual differences in non-verbal number acuity correlate with maths achievement. Nature. 2008; 455:665-668

[82] hattie j, biggs j, purdie n. Effects of learning skills interventions on student learning : a meta-analysis. Rev Educ Res. 1996; 66:99-136

[83] hayter s, scott e, mclaughlin tf, weber kp. The use of a modified direct instruction flashcard system with two high school students with developmental disabilities. J Dev Phys Disabil. 2007; 19:409-415

[84] henry jh, van amelsvoort t, morris r, murphy dg, murphy kc. An investigation of the neuropsychological profile in adults with velo-cardio-facial syndrome (VCFS). Neuropsychologia. 2002; 40:471-478

[85] herrera an, bruno a, gonzález c, moreno l, sanabria h. Addition and subtraction by students with Down syndrome. Int J Math Educ Sci Technol. 2011; 42:13-35

[86] hodapp rm, dykens em. Studying behavioral phenotypes : issues, benefits, challenges. In: emersone, hattonc, thompsont, parmentertr, editors. The international handbook of applied research in intellectual disabilities. Chichester:John Wiley & Sons Ltd.; 2004. p. 203-220

[87] hodapp rm, desjardin jl, ricci la. Genetic syndromes of mental retardation. should they matter for the early interventionist ?. Infants Young Child. 2003; 16:152-160

[88] holmes j. Developmental disorders and interventions. Adv Child Dev Behav. 2010; 39:2-272

[89] hord c, bouck ec. Review of academic mathematics instruction for students with mild intellectual disability. Educ Training Autism Dev Disabil. 2012; 7:389-400

[90] hubbard em, piazza m, pinel p, dehaene s. Interactions between number and space in parietal cortex. Nature Reviews, Neuroscience. 2005; 6:435-448

[91]inserm. Dyslexie, dysorthographie, dyscalculie : Bilan des données scientifiques - Synthèse et Recommandations. Collection Expertise collective. Paris:Éditions Inserm; 2007.

[92] jacobson c, shearer j, habel a, kane f, tsakanikos e, et coll. . Core neuropsychological characteristics of children and adolescents with 22q11.2 deletion. J Intellect Disabil Res. 2010; 54:701-713

[93] jarvis hl, gathercole se. Verbal and non-verbal working memory and achievements on national curriculum tests at 11 and 14 years of age. Educ Child Psychol. 2003; 20:123-140

[94] jordan ke, baker j. Multisensory information boosts numerical matching abilities in young children. Dev Sci. 2011; 14:205-213

[95] käser t, busetto ag, baschera gm, kohn j, kucian k, et coll. . Modelling and optimizing the process of learning mathematics. Proceedings of Intelligent Tutoring Systems (Chania, Greece, June 14-18, 2012). 2012; 389-398

[96] käser t, busetto ag, solenthaler b, baschera gm, kohn j, et coll. . Modelling and optimizing mathematics learning in children. Int J Artif Intell Educ. 2013; 23:115-135

[97] karvonen m, flowers c, wakeman sy. Factors associated with access to the general curriculum for students with intellectual disability. Curr Issues Educ. 2013; 16:1-18

[98] kaufman el, lord mw, reese tw, volkmann j. The discrimination of visual number. Am Jo Psychol. 1949; 62:498-535

[99] kearns dm, fuchs m. Does cognitively focused cognitive instruction improve the academic performance of low achieving students. Exceptional Children. 2013; 79:263-290

[100] kliewer c, biklen d, kasa-hendrickson c. Who may be literate ? Disability and resistance to the cultural denial of competence. Am Educ Res J (Summer). 2006; 43:163-192

[101] krajcsi a, lukacs a, igacs j, racsmany m, pleh c. Numerical abilities in Williams syndrome : dissociating the analogue magnitude system and verbal retrieval. J Clin Exp Neuropsychol. 2009; 31:439-446

[102] kroesbergen eh, van luit jeh. Mathematics interventions for children with special educational needs : A meta-analysis. Remedial Special Educ. 2003; 24:97-114

[103] kroesbergen eh, van luit jeh. Constructivist mathematics education for students with mild mental retardation. Eur J Special Needs Educ. 2005; 20:107-116

[104] kucian k, von aster m, loenneker t, dietrich t, martin e. Development of neural networks for exact and approximate calculation : a FMRI study. Dev Neuropsychol. 2008; 33:447-473

[105] kunsch ca, jitendra ak, sood s. The effects of peer-mediated mathematics instruction for students with disabilities : A review of the literature. Learn Disabil Res Pract. 2007; 22:1-12

[106] kyttälä m. Visuospatial working memory in adolescents with poor performance in mathematics : variation depending on reading skills. Educ Psychol. 2008; 28:273-289

[107] kyttälä m, aunio p, lehto je, van luit jeh, hautamäki j. Visuospatial working memory and early numeracy. Educ Child Psychol. 2003; 20:65-76

[108] lecointre as, lépine r, camos v. Développement et troubles des processus de quantification. In: noëlmp, editors. La dyscalculie : Trouble du développement numérique de l’enfant. Marseille:Solal; 2005. p. 41-75

[109] lemaire p, abdi h, fayolm m. The role of working memory resources in simple cognitive arithmetic. Eur J Cogn Psychol. 1996; 8:73-103

[110] lenhard a, lenhard w, schug m, kowalski a. Computerbasierte Mathematikförderung mit den “Rechenspielen mit Elfe und Mathis I” - Vorstellung und Evaluation eines Computerprogramms für Erst- bis Drittklässler. Zeitschrift für Entwicklungspsychologie und Pädagogische Psychologie. 2011; 43:79-88

[111] lenhard w, lenhard a. Rechenspiele mit Elfe und Mathis I [CD-ROM]. Göttingen:Hogrefe; 2010.

[112] lenhard w, lenhard a, lingel k. Rechenspiele mit Elfe und Mathis II [CD-ROM]. Göttingen:Hogrefe; 2010.

[113] lepach ac, petermann f. Nonverbal and verbal learning : a comparative study of children and adolescents with 22q11 deletion syndrome, non-syndromal Nonverbal Learning Disorder and memory disorder. Neurocase. 2011; 17:480-490

[114] libertus me, feigenson l, halberda j. Preschool acuity of the approximate number system correlates with school math ability. Dev Sci. 2011; 14:129-300

[115] libertus me, feigenson l, halberda j, landau b. Understanding the mapping between numerical approximation and number words : evidence from Williams syndrome and typical development. Dev Sci. 2014; 17:905-919

[116] link t, moeller k, huber s, fischer u, nuerk hc. Walk the number line – An embodied training of numerical concepts. Trends Neurosci Educ. 2013; 2:74-84

[117] malofeeva e. Meta-analysis of mathematics instruction with young children. University of Notre Dame; 2005.

[118] mazzocco mmm. When a genetic disorder is associated with learning disabilities. In: mazzoccommm, rossjl, editors. Neurogenetic developmental disorders : Manifestation and identification in childhood. Cambridge, MA:The MIT Press; 2007. p. 415-436

[119] mazzocco mm, feigenson l, halberda j. Preschoolers’ precision of the approximate number system predicts later school mathematics performance. PLoS One. 2011; 6:e23749

[120] meyer ml, salimpoor vn, wu ss, geary dc, menon v. Differential contribution of specific working memory components to mathematics achievement in 2nd and 3rd graders. Learn Individ Differ. 2010; 20:101-109

[121] montgomery jk. Current status of evidence-based practices for low-incidence disabilities : Introduction to the special series. Commun Disord Q. 2006; 28:37-38

[122] moser-opitz e, garrote a, ratz c. Mathematische Kompetenzen von Schülerinnen und Schülern mit dem Förderschwerpunkt Geistige Entwicklung. Sonderpadagogische Forderung Heute. 2014; 59:19-31

[123] moss em, batshaw ml, solot cb, gerdes m, mcdonald-mcginn dm, et coll. . Psychoeducational profile of the 22q11.2 microdeletion : a complex pattern. J Pediatr. 1999; 134:193-198

[124] moyer rs, landauer tk. Time required for judgments of numerical inequality. Nature. 1967; 215:1519-1520

[125] murphy mm, mazzocco mm. Rote numeric skills may mask underlying mathematical disabilities in girls with fragile X syndrome. Dev Neuropsychol. 2008; 33:345-364

[126] nye j, fluck m, buckley s. Counting and cardinal understanding in children with Down syndrome and typically developing children. Downs Syndrome Res Pract. 2001; 7:68-78

[127] nys j, ventura p, fernandes t, querido l, leybaert j, et coll. . Does math education modify the approximate number system ? A comparison of schooled and unschooled adults. Trends Neurosci Educ. 2013; 2:13-22

[128] o’hearn k, landau b. Mathematical skill in individuals with Williams syndrome : evidence from a standardized mathematics battery. Brain Cogn. 2007; 64:238-246

[129] o’hearn k, luna b. Mathematical skills in Williams syndrome : insight into the importance of underlying representations. Dev Disabil Res Rev. 2009; 15:11-20

[130] o’hearn k, hoffman je, landau b. Small subitizing range in people with Williams syndrome. Visual Cogn. 2011; 19:289-312

[131]ocde. De la formation initiale à la vie active : faciliter les transitions. OCDE; Paris:2000;

[132]ocde. Analyse des politiques d’éducation. 2003.

[133]ocde. Élèves présentant des déficiences, des difficultés et des désavantages sociaux. 2008.

[134]ocde. Résultats du PISA 2009 : savoirs et savoir-faire des élèves. Performance des élèves en compréhension de l’écrit, en mathématiques et en sciences. 2011.

[135]ocde. Des compétences pour la vie ? Principaux résultats de l’évaluation des compétences des adultes. 2013.

[136] odom s, brantlinger e, gersten r, horner r, thompson b, et coll. . Research in special education : Scientific methods and evidence-based practices. Exceptional Children. 2005; 71:137-148

[137]onfrih. Rapport triennal de l’Observatoire National sur la Formation, la Recherche et l’Innovation sur le Handicap. 2011.

[138]ost. Indicateurs bibliométriques de la recherche dans le domaine du handicap. Convention n^o 08/2381; 2008;

[139] ostergren r. Mathematical learning disability. Cognitive conditions, developement and predictions. Linköping University; 2013.

[140] passolunghi mc, cornoldi c. Working memory failures in children with arithmetical difficulties. Child Neuropsychol. 2008; 14:387-400

[141] passolunghi mc, lanfranchi s. Domain-specific and domain-general precursors of mathematical achievement : a longitudinal study from kindergarten to first grade. Br J Educ Psychol. 2012; 82:42-63

[142] paterson s. Language and number in Down syndrome : the complex developmental trajectory from infancy to adulthood. Downs Syndrome Res Pract. 2001; 7:79-86

[143] paterson sj, girelli l, butterworth b, karmiloff-smith a. Are numerical impairments syndrome specific ? Evidence from Williams syndrome and Down’s syndrome. J Child Psychol Psychiatry. 2006; 47:190-204

[144] perrig wj, hollenstein m, oelhafen s. Can we improve fluid intelligence with training on working memory in persons with intellectual disabilities ?. J Cogn Educ Psychol. 2009; 8:148-164

[145] persson c, niklasson l, oskarsdottir s, johansson s, jonsson r, et coll. . Language skills in 5-8-year-old children with 22q11 deletion syndrome. Int J Lang Commun Disord. 2006; 41:313-333

[146] petitpierre g, masse m, martini-willemin bm, delessert y. A complementarity of social and legal perspectives on what is abusive practice and what constitutes abuse. J Policy Pract Intellect Disabil. 2013; 10:196-206

[147] petitpierre g, gremaud g, veyre a, bruni i. Les apprentissages à l’âge adulte, ce qu’en disent les personnes avec une déficience intellectuelle. 2014; (www.deficiences-intellectuelles.ch).

[148] pintrich pr, zeidner m. Handbook of Self-Regulation. San Diego, CA:Academic Press; 2000.

[149] plaisance e. Conférence de consensus 2008. Scolariser les élèves en situation de handicap : pistes pour la formation. Recherche et Formation. 2009; 61:11-40

[150] prado j, mutreja r, both jr. Developmental dissociation in the neural responses to simple multiplication and substraction problems. Dev Sci. 2014; 17:537-552

[151] price gr. Why mental arithmetic counts : Brain activation during single digit arithmetic predicts high school math scores. J Neurosci. 2013; 33:156-163

[152] rao s, mallow l. Using simultaneous prompting procedure to promote recall of multiplication facts by middle school students with cognitive impairment. Educ Train Dev Disabil. 2009; 44:80-90

[153] regnaux jp, guay vr, marsal c. Evidence based practice ou la pratique basée sur les preuves en rééducation. Kinésithérapie La Revue. 2009; 9:55-61

[154] riccio ca, sullivan jr, cohen mj. Neuropsychological assessment and intervention for childhood and adolescent disorders. Hoboken:Wiley; 2010. 744p.

[155] romainville m. Conscience, métacognition, apprentissage : le cas des compétences méthodologiques. In: ponsf, doudinpa, editors. La conscience chez l’enfant et chez l’élève. Québec:Presses de l’Université du Québec; 2007. p. 108-130

[156] rose sa, feldman jf, jankowski jj. Modeling a cascade of effects : the role of speed and executive functioning in preterm/full-term differences in academic achievement. Dev Sci. 2011; 14:1161-1175

[157] rousselle l, dembour g, noel mp. Magnitude representations in Williams syndrome : differential acuity in time, space and number processing. PLoS One. 2013; 8:e72621

[158] rynders j, abery bh, spiker d, olive ml, sheran cp, et coll. . Improving educational programming for individuals with Down syndrome : engaging the fuller competence. Down Syndrome Quart. 1997; 2:1-11

[159] saldana d. Interactive assessment of metacognition : exploratory study of a procedure for persons with severe mental retardation. Eur J Psychol Educ. 2004; 19:349-364

[160] samuel j. Age appropriateness : Occasionnel Paper I. 1999.

[161] sante ad, mclaughlin tf, weber kp. The use and evaluation of a direct instruction flash card strategy on multiplication math facts mastery with two students with developmental disabilities and attention deficit hyperactivity disorder. J Precision Teaching Celeration. 2001; 17:68-75

[162] schuelka mj. Excluding students with disabilities from the culture of achievement : the case of the TIMSS, PIRLS, and PISA. J Educ Policy. 2013; 28:216-230

[163] sella f, lanfranchi s, zorzi m. Enumeration skills in Down syndrome. Res Dev Disabil. 2013; 34:3798-3806

[164] shams l, seitz ar. Benefits of multisensory learning. Trends Cogn Sci. 2008; 12:411-417

[165] shepperdson b. Attainments in reading and number of teenagers and young adults with Down’s syndrome. Downs Syndrome Res Pract. 1994; 2:97-101

[166] simon tj. A New Account of the Neurocognitive Foundations of Impairments in Space, Time and Number Processing in Children with Chromosome 22q11.2 Deletion Syndrome. Dev Disabil Res Rev. 2008; 14:52-58

[167] simon tj. Clues to the foundations of numerical cognitive impairments : Evidence from genetic disorders. Dev Neuropsychol. 2011; 36:788-805

[168] simon tj, burg-malki m, gothelf d. Cognitive and Behavioral characteristics of children with chromosome 22q11.2 deletion syndrome. In: mazzoccommm, rossjl, editors. Neurogenetic developmental disorders : variation of manifestation in childhood. Cambridge, MA:MIT Press; 2005. p. 163-198

[169] simon tj, takarae y, deboer t, mcdonald-mcginn dm, zackai eh, et coll. . Overlapping numerical cognition impairments in children with chromosome 22q11.2 deletion or Turner syndromes. Neuropsychologia. 2008; 46:82-94

[170] smith a. Making mathematics count. The report of professor Adrian Smith’s inquiry into post-14 mathematics education. HMSO; 2004.

[171] spelke es, tsivkin s. Language and number : A bilingual study. Cognition. 2001; 78:45-88

[172] szücs dã, devine a, soltesz f, nobes a, gabriel f. Cognitive components of a mathematical processing network in 9-year-old children. Dev Sci. 2014; 17:506-524

[173] temple e, posner mi. Brain mechanisms of quantity are similar in 5-year-old children and adults. Proc Natl Acad Sci USA. 1998; 95:7836-7841

[174] thévenot c, masson s. Améliorer les compétences numériques. ANAE. 2013; 123:

[175] thioux m, pesenti m, costes n, de volder a, seron x. Task-independent semantic activation for numbers and animals. Cogn Brain Res. 2005; 24:284-290

[176] turner s, alborz a. Academic attainments of children with Down’s syndrome : a longitudinal study. Br J Educ Psychol. 2003; 73:563-583

[177] turner s, alborz a, gayle v. Predictors of academic attainments of young people with Down’s syndrome. J Intellect Disabil Res. 2008; 52:380-392

[178] van herwegen j, ansari d, xu f, karmiloff-smith a. Small and large number processing in infants and toddlers with Williams syndrome. Dev Sci. 2008; 11:637-643

[179] van nieuwenhoven c, grégoire j, noël mp. Le TEDI-MATH : test diagnostique des compétences de base en mathématiques. Paris:ECPA; 2001.

[180] vaughn s, wanzek j, murry cs, roberts g. Intensive interventions for students struggling in reading and mathematics : a practice guide. RMC Research Corporation, Center on Instruction; Portsmouth, NH:2012;

[181] veenman mvj, van hout-wolters bham, afflerbach p. Metacognition and learning : conceptual and methodological considerations. Metacogn Learn. 2006; 1:3-14

[182] vilette b, meyer s, joay-arrouquet j. Children’s mapping between symbolic and analogical representations of number : evidence from a training study in children with Down’s syndrome. 28^th International Congress of Applied Psychology; 8-13 juillet 2014; Paris: France.

[183] von aster mg, dellatolas g. ZAREKI-R : Batterie pour l’évaluation du traitement des nombres et du calcul chez l’enfant ; Adaptation française. ECPA; Paris:2006;

[184] wendling bj, mather n. Essentials of evidence-based academic interventions. John Wiley; New Jersey, NJ:2009;

[185] wilson a, räsänen p. Effective interventions for numeracy difficulties/disorders. Encyclopedia of Language and Literacy Development. London, ON:Canadian Language and Literacy Research Network; 2009; 1-11

[186] wilson aj, dehaene s, pinel p, revkin sk, cohen l, et coll. . Principles underlying the design of “The Number Race”, an adaptive computer game for remediation of dyscalculia. Behav Brain Functions. 2006; 2:19

[187] xin yp, jitendra a, deatline-buchman a. The effects of mathematical word problem-solving instruction on middle school students with learning problems. J Spec Educ. 2005; 39:181-192

[188] zigler e. Familial mental retardation : a continuing dilemma. Science. 1967; 155:292-298

[189] zorzi m, priftis k, umiltã c. Neglect disrupts the mental number line. Nature. 2002; 417:138-139

[190] zorzi m, priftis k, meneghello f, marenzi r, umilta c. The spatial representation of numerical and non-numerical sequences : evidence from neglect. Neuropsychologia. 2006; 44:1061-1067