| |
| Med Sci (Paris). 2010 January; 26(1): 57–64. Published online 2010 January 15. doi: 10.1051/medsci/201026157.Approche multi-échelle appliqué à la modélisation de l’activité électrique du coeur Philippe Comtois,1 Mark Potse,2 and Alain Vinet2* 1Institut de cardiologie de Montréal, Institut de génie biomédical, Faculté de médecine, Université de Montréal, Montréal, Canada 2Institut de génie biomédical, Faculté de médecine, Université de Montréal, Centre de recherche de l’Hôpital du Sacré-Coeur de Montréal, 5400, boulevard Gouin Ouest, Montréal (Quebec), H4J 1C7 Canada |
La modélisation de l’activité électrique cardiaque peut être circonscrite à la description des mécanismes qui régissent la formation des potentiels d’action par les myocytes, cellules d’un volume de quelques 3 000 μm3. Elle peut aussi appréhender la dynamique de la propagation du courant intracellulaire circulant dans les jonctions résistives formées par les connexines et du courant qui se propage dans le milieu extracellulaire. Le déclenchement d’une arythmie peut dépendre à la fois de la structure du tissu et de l’influence mutuelle de l’excitabilité et de la repolarisation des myocytes. La modélisation peut concerner aussi bien le tissu myocardique isolé que le cœur entier qui occupe un volume d’environ 100 cm3 chez l’humain adulte. Pour faire le lien entre l’activité de ces tissus et l’électrocardiogramme (ECG) reflétant sa transmission au torse, il faut insérer le cœur dans un modèle représentatif du torse. Cela revient donc pour l’ensemble des travaux de modélisation à couvrir un minimum de six ordres de grandeur, sans compter les travaux sur la représentation des diverses protéines participant à la genèse des courants et au maintien de l’équilibre ionique [
1]. Quant à la durée de ces processus, les intervalles de temps s’échelonnent de la milliseconde, si l’on considère l’activation des canaux ioniques, à plusieurs minutes si l’on s’intéresse au déclenchement et au développement des arythmies. L’intégration de multiples échelles temporelles et spatiales représente un défi commun à la modélisation de tous les systèmes physiologiques complexes. Ceci a suscité diverses initiatives internationales comme les projets du physiome1 et de l’humain virtuel qui veulent donner accès, dans un environnement intégré, aux données expérimentales et cliniques aussi bien qu’aux modèles concernant diverses échelles de modélisation [
2,
3]. Nous discuterons brièvement de trois contextes de modélisation où la nature des questions exige des niveaux différents de complexité. |
Modèles et dynamique du cardiomyocyte isolé La complexité des modèles cellulaires s’accroît sans cesse : dans le cas du cardiomyocyte par exemple, il faudrait inclure une description détaillée de tous les types de canaux ioniques, des pompes et échangeurs ioniques insérés dans la membrane cytoplasmique ; il faudrait aussi considérer la compartimentation intracellulaire qui intervient par exemple, dans la dynamique du calcium intracellulaire ou dans la modulation adrénergique et cholinergique [
4–
5]. Ce degré de réalisme est essentiel pour analyser les conséquences de mutations génétiques touchant les canaux ioniques ou l’action de médicaments spécifiques sur les propriétés du potentiel d’action. Un tel raffinement engendre des modèles trop complexes qui ne sont plus accessibles à un traitement analytique, et ne peuvent plus être étudiés que par simulation numérique. Le nombre de paramètres dont il faut fixer la valeur peut atteindre la centaine. En outre, faute de données expérimentales appropriées, des valeurs arbitraires sont attribuées à plusieurs d’entre eux. Des formulations alternatives se font concurrence sans qu’on puisse trouver de critères pour les distinguer. C’est d’ailleurs l’un des objectifs du projet du physiome cardiaque que de constituer un tel catalogue de modèles validés [
6]. Enfin, tant chez les espèces que chez les individus, le changement des caractéristiques cellulaires dans le temps remet en question la généralisation des résultats obtenus par une série de simulations numériques. Une approche alternative consiste à tenter d’établir des résultats génériques à partir de modèles simplifiés. En effet, plusieurs des résultats de modélisation qui ont eu un impact important ont été obtenus dans des modèles extrêmement simples qui ne cherchaient pas à reproduire la complexité du tissu cardiaque, mais plutôt à mettre en relief le rôle central de certaines de ses propriétés [
7]. Considérons le problème d’une cellule stimulée. Après l’administration d’un stimulus provoquant un potentiel d’action, il y a une période réfractaire pendant laquelle un second stimulus ne pourra pas susciter une nouvelle réponse active. Une analyse superficielle conclura que la cellule devrait répondre à chaque stimulus par des potentiels d’action identiques tant que la période de stimulation reste supérieure à la période réfractaire. Cependant, la durée de la période réfractaire dans les cellules cardiaques diminue généralement avec l’augmentation du rythme, ce qui permet de maintenir des rythmes plus rapides quand cela est nécessaire. Si la durée du potentiel d’action ne dépend que de l’intervalle diastolique - le temps écoulé entre la fin de la période réfractaire et l’application du stimulus (Figure 1B) - la relation entre la durée du potentiel d’action et la prématurité du stimulus peut être résumée par une seule courbe que l’on nomme courbe de restitution (Figure 1C), et la dynamique de l’entraînement par l’itération d’une seule équation (l’intervalle diastolique d’un nouveau stimulus est donné par une fonction qui ne dépend que de l’intervalle diastolique du stimulus précédent). L’analyse de ce système démontre que, selon la forme de la courbe de restitution, l’augmentation de la fréquence d’entraînement peut mener à des régimes stables où la réponse alterne entre des potentiels d’action longs et courts. Ce résultat est confirmé par la simulation de modèles ioniques2 et par des expériences sur des cellules isolées. Parce que l’apparition d’une alternance est souvent un prélude au déclenchement d’arythmie, ce résultat a attiré l’attention des chercheurs en suggérant que certaines arythmies pourraient être prévenues par des agents pharmacologiques modifiant la courbe de restitution des myocytes [
8]. Ce modèle simple a donné naissance à des hypothèses qui restent à valider avec des modèles plus complexes et des préparations expérimentales adéquates. Certes, les modèles simplifiés ne constituent pas des substituts aux modèles plus complexes et réalistes qui sont essentiels pour explorer, par exemple, l’action d’un agent pharmacologique particulier [
9]. Ils se définissent plutôt comme une approche complémentaire en vue d’identifier des phénomènes génériques.
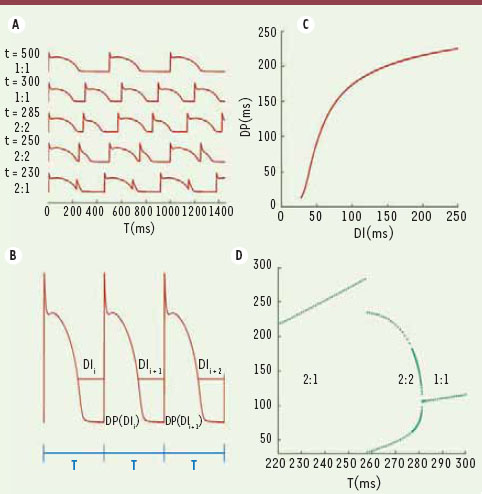
 | Figure 1.
Réponse à l’entraînement d’un modèle de myocyte isolé. A. Évolution de la réponse à l’entraînement d’un modèle de myocyte ventriculaire cardiaque en fonction de la période de stimulation [
30]. Chaque stimulus est une impulsion de courant de 1 ms appliquée avec une période fixe T, dont la valeur en ms apparaît à gauche de chaque graphique. La périodicité de la réponse est indiquée par le couple a : b, a = nombre de stimulus, b = nombre de réponses actives. B. Si la durée du potentiel d’action (DP) dépend uniquement de l’intervalle diastolique précédent (DI), la réponse à l’entraînement est décrite par le système itéré DI i+1 = T-DP(DI i). C. Fonction DP(DI) du modèle ionique. D. Réponse à l’entraînement prédite par le modèle itéré. Pour chaque T, le graphique montre les valeurs de DI de la réponse stable. |
|
Microstructure et arythmies auriculaires Arythmies et processus de réentrée Pendant la propagation d’un front d’activation, les myocytes activés fournissent du courant à leurs voisins qui, lorsqu’ils atteignent leur seuil d’activation, produisent à leur tour un potentiel d’action et deviennent des sources permettant à l’excitation de continuer à se propager. Cet échange de courant se fait à travers des jonctions intercellulaires que l’on peut considérer comme équivalentes à des résistances électriques [
10]. Normalement, l’activation électrique est produite spontanément par le nœud sinusal 3,, elle se propage des oreillettes aux ventricules où elle se termine. Tout le tissu revient alors au repos jusqu’au déclenchement du battement suivant. Les arythmies cardiaques résultent de la désorganisation de la propagation de cette activité électrique. L’un des principaux mécanismes d’arythmie est le phénomène de réentrée : il correspond à la propagation soutenue d’un front d’activation électrique autour d’un obstacle fonctionnel ou anatomique. Dans le cas d’un obstacle anatomique, il peut s’agir d’une macro-réentrée : le front d’activation circule autour d’une valve, comme dans certaines formes d’arythmies auriculaires, ou autour d’une région du tissu ventriculaire devenue inexcitable à la suite d’une ischémie. Pour amorcer la réentrée, le front de propagation doit contourner une portion du circuit temporairement réfractaire et y revenir après un temps assez long pour que cette région soit de nouveau excitable. Par la suite, la réentrée sera pérennisée si le temps nécessaire à la circulation du front est supérieur à la période réfractaire partout le long du circuit. On a montré qu’un obstacle, de diamètre aussi petit que 0,6 mm, pouvait ancrer la réentrée 4 dans des cultures de tissu - bien que la dimension minimale fût dix fois plus grande dans l’oreillette du chien [
11,
12]. Toute modification du tissu qui augmente la probabilité de la formation d’un bloc local ou qui diminue la vitesse de propagation autour d’un obstacle sera favorable au déclenchement et au maintien de réentrées. Impact du processus fibrotique sur l’arythmie La structure du tissu est assurée par la matrice extracellulaire qui sert de squelette auquel les cardiomyocytes sont attachés. La fibrose, une forme de remodelage structurel causée par l’augmentation du collagène extracellulaire, a été associée au déclenchement et à la perpétuation de la fibrillation auriculaire (FA) [
13]. Plusieurs pathologies peuvent provoquer la fibrose : cardiomyopathies, maladies de la valve mitrale, myocardites, hypertension artérielle. L’accroissement naturel de la fibrose avec le temps pourrait expliquer la prévalence croissante de la FA dans la population âgée. La fibrose a aussi été associée à des troubles de conduction électrique. Dans un modèle expérimental de défaillance cardiaque induite par la stimulation rapide et prolongée des ventricules, l’augmentation de la pression auriculaire entraîne un taux important de mort cellulaire et le remplacement des myocytes nécrosés par du collagène, ce qui correspond à la fibrose [
14]. Ce remodelage engendre l’isolation électrique des myocytes voisins et forme des barrières à la propagation propices au processus de réentrée [
15]. L’interaction onde-obstacle peut augmenter la courbure de l’onde électrique, ce qui ralentit sa propagation et module la durée du potentiel d’action [
16,
17]. Dans une étude théorique, la présence de petites zones de fibrose avait pour effet de diminuer la complexité et la vitesse de rotation de l’activité réentrante sans toutefois toujours servir d’ancrage à l’onde électrique [
18]. Deux exemples de comportement avec des caractéristiques de fibroses différentes sont présentés dans la Figure 2. La dimension minimale d’un obstacle permettant de stabiliser la réentrée est très dépendante de la conductivité du tissu et des niveaux d’expression des canaux ioniques [17]. Un modèle stochastique de fibrose a prédit que le bloc de propagation de l’activité électrique auriculaire était sensible non seulement à l’importance de la fibrose, mais aussi au détail de son organisation spatiale [
19]. La modélisation de l’effet de la fibrose exige donc une représentation réaliste de la microstructure avec une résolution supérieure au diamètre de la cellule cardiaque qui est de l’ordre de 10 μm. Dans une première approche de modélisation, on a introduit dans un modèle bidimensionnel la distribution spatiale des cardiomyocytes et du collagène observée sur des coupes histologiques de tissu auriculaire canin avec une résolution de l’ordre d’un micron (Figure 3A, B). L’activité électrique a été simulée en utilisant une approche de milieu continu (qui néglige la séparation entre les myocytes) et un modèle ionique (voir note 2) reproduisant les courants mesurés dans les myocytes auriculaires canins. Un exemple de propagation électrique est illustré par la Figure 3C sous la forme d’une carte isochronale des temps d’activation. Les sites en noir correspondent à des régions connectées mais non activées en raison d’une fibrose plus importante. Cette approche permet d’étudier l’impact de la fibrose sur la propagation et offre la possibilité d’établir une activité réentrante à la suite d’une activité ectopique rapide. Elle compte cependant plusieurs limitations. Premièrement, l’utilisation d’un modèle de tissu bidimensionnel limite les zones où la propagation peut se perpétuer, comme cela a été démontré dans un modèle théorique [19]. Il sera donc nécessaire de procéder à une reconstruction tridimensionnelle du tissu cardiaque en s’appuyant sur une résolution assez fine pour représenter la fibrose et une dimension assez étendue pour permettre une réentrée. De plus, il est difficile à partir des coupes histologiques de séparer les zones où la matrice extracellulaire est normale de celles où la fibrose provoque une déconnexion des cardiomyocytes. Enfin, la modélisation de l’activité électrique à cette échelle devra éventuellement tenir compte de la répartition des jonctions intercellulaires, des changements de propriétés ioniques pouvant survenir lors de pathologies et du fait que le tissu est une mosaïque de myocytes distincts.
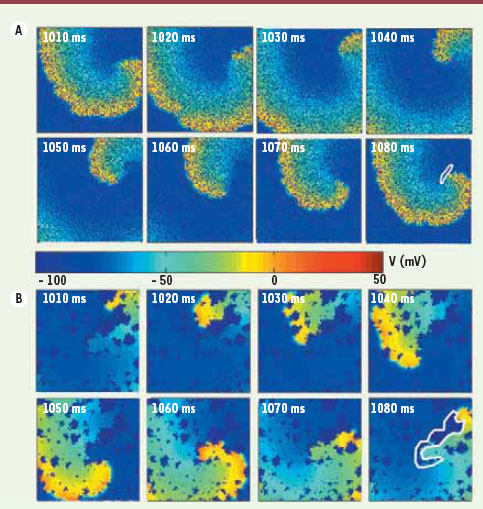
 | Figure 2.
Exemples de réentrée en présence de fibrose. A. Réentrée sur un substrat auriculaire 2D de 3 cm x 3 cm avec petits amas de fibrose (petites zones en bleu foncé la courbe blanche. portion activée du tissu où V > - 50 mv). Les différents panneaux correspondent à l’état du potentiel transmembranaire (V) aux temps indiqués. La trajectoire de la zone regénératrice interne est indiquée par une courbe blanche dans le dernier panneau. La période de rotation est de ~ 73 ms. B. Réentrée sur un substrat auriculaire 2D avec gros amas de fibrose. La présentation est la même qu’en A. Dans cet exemple, la réentrée est clairement ancrée sur un ensemble d’amas se trouvant à l’intérieur de la courbe blanche. L’augmentation de la longueur de la trajectoire comparativement au cas en A due à l’ancrage de la réentrée est responsable de la plus grande période de rotation autour de ~ 92 ms. |
 | Figure 3.
Modélisation d’un tissu fibrotique réel. A. Coupe histologique (3,8 × 2,4 cm) du tissu auriculaire canin d’un animal en défaillance cardiaque (coloration au trichrome de Masson). Les cardiomyocytes sont colorés en rouge et le collagène, un des constituants principaux de la matrice extracellulaire, en vert. B. Représentation binaire des myocytes (noir) et de la fibrose (blanc). C. Simulation de la propagation d’une onde d’activation dans le tissu reconstruit avec une résolution spatiale de 75 μm. Le code couleur correspond aux temps d’activation de chaque point du tissu. |
|
Modèle cœur-torse et la reproduction de l’ECG L’ECG, le plus commun des signaux électrophysiologiques, est utilisé aussi bien pour les examens de routine que pour le suivi du patient dans diverses circonstances. Il permet d’analyser le rythme cardiaque, pour détecter les arythmies ou évaluer l’état du système nerveux autonome [
20]. Il renseigne aussi sur l’état du tissu cardiaque, notamment quant à la présence d’une ischémie ventriculaire. Du point de vue électrique, le torse est un milieu résistif où les courants produits par les myocytes circulent et causent des différences de potentiel qui sont mesurées par l’ECG. L’interprétation de l’ECG consiste à déduire l’évolution de l’excitation et de la repolarisation dans le tissu cardiaque à partir des potentiels électriques mesurés sur le torse [
21]. Implicitement, c’est ce que fait tout clinicien qui établit un diagnostic en examinant les trois ou douze dérivations d’un ECG. Dans le cas du problème direct, on cherche plutôt à obtenir l’ECG à partir d’un modèle permettant de simuler l’évolution de l’activité électrique des myocytes. Les courants produits par les cellules cardiaques sont calculés et sont ensuite utilisés pour reconstruire l’ECG. Plusieurs caractéristiques de l’ECG peuvent être simulées avec un modèle aussi simple qu’un dipôle électrique5 d’intensité variable se déplaçant dans le cœur. Cependant, certains problèmes ne peuvent être abordés qu’avec un modèle qui représente les flux ioniques provenant des myocytes et qui incorpore leurs interactions avec les flux circulant dans le milieu extracellulaire cardiaque et dans le torse. Cela est vrai pour les maladies affectant les canaux ioniques ou pour comprendre la genèse d’arythmies survenant en bordure d’une région ischémique où l’absence de perfusion altère la composition ionique des milieux intra et extracellulaires et l’état des myocytes [
22]. Actuellement, seules de petites préparations permettent de représenter tous les myocytes et la microstructure du tissu cardiaque. À l’échelle cœur-torse, l’alternative consiste à considérer les milieux extracellulaires et intracellulaires comme des continuums [
23]. Dans l’approche dite bidomaine, les milieux extracellulaire et intracellulaire cardiaques sont coextensifs (chaque nœud du modèle représente à la fois un volume de milieu intra- et extracellulaire, les deux étant couplés par les membranes des myocytes) (Figure 4A) [
24]. On définit ensuite un maillage où les tenseurs de résistivité et les propriétés membranaires sont définis à chaque nœud. Quelque vingt-six millions de nœuds sont nécessaires pour construire un modèle de cœur humain avec une résolution de 0,2 mm (Figure 4B) [
25]. Le tenseur de résistivité tient compte du fait que les conductivités intra et extracellulaires sont plus grandes dans la direction des fibres, et que cette direction change entre l’endocarde et l’épicarde. Les propriétés membranaires doivent être choisies pour reproduire les différents types de myocytes qui se trouvent dans le muscle cardiaque. La grande diversité des durées de potentiel d’action détermine une grande partie des formes d’onde détectées sur l’ECG.
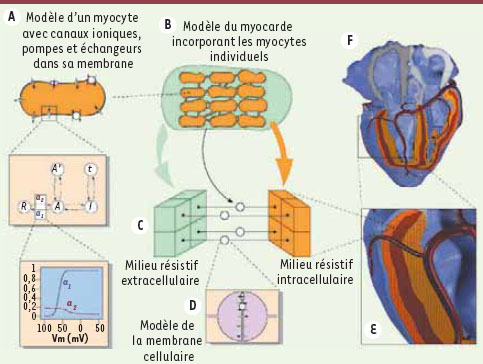
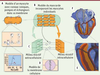 | Figure 4.
Différentes échelles de modélisation. A. La membrane du myocyte porte des canaux ioniques, des pompes et des échangeurs d’ions. Chaque canal peut occuper différents états qui correspondent aux différentes configurations des protéines qui le forment. L’exemple montre un canal qui peut prendre cinq configurations : les transitions entre états se font avec une probabilité qui peut dépendre du potentiel membranaire. Dans l’exemple, a1 et a2 sont des taux de transition fonction du potentiel membranaire. B. Pour modéliser le tissu, on remplace les cellules individuelles par un milieu résistif intracellulaire séparé par une membrane d’un milieu résistif extracellulaire. C, D. Dans le modèle bidomaine, le tissu est divisé en éléments de volume. Chaque élément représente des volumes de tissus intra et extracellulaires couplés par une surface membranaire. E. En couplant des millions de volumes élémentaires (cubes de 0,2 mm 3 dans ce modèle de cœur humain [ 25]), on construit un modèle macroscopique. Les tenseurs de conductivité électrique intra et extracellulaire, ainsi que les paramètres du modèle ionique, sont définis pour chaque cube. La direction des fibres cardiaques, qui gouverne les tenseurs de conductivité, est indiquée par les lignes noires. F. Vue postérieure du modèle de cœur humain : une partie de la paroi inférieure ou diaphragmatique est enlevée pour montrer l’intérieur. |
Ce type de modèle aspire donc à simuler l’ECG en utilisant seulement des connaissances physiologiques propres aux canaux ioniques et à la structure du tissu (Figure 5). Ce que l’on connaît de la microstructure du tissu cardiaque devrait être suffisant pour reproduire les potentiels électriques mesurés sur le torse. Cette ambition représente à la fois la force et la faiblesse de cette approche. C’est une force, car cela peut montrer que les connaissances traditionnelles ne suffisent pas pour comprendre complètement les formes d’onde de l’ECG normal [
26]. Les résultats de simulation suggèrent que la dispersion spatiale des propriétés de repolarisation doit être plus grande que celle qui est observée dans des cellules isolées. C’est une faiblesse car, en contrepartie, l’ECG simulé par les modèles les plus avancés semble pour le moment moins réaliste que celui que produisent des modèles plus anciens ou plus simples [
27] où les sources utilisées pour reproduire un ECG normal sont déterminées empiriquement plus qu’elle ne se fondent directement sur des données expérimentales. Le but ultime est de disposer d’un modèle cœur-torse réaliste (Figure 5) qui puisse être adapté à chaque patient pour valider le diagnostic établi à partir de l’ECG ou guider la thérapie, comme le choix du site d’implantation des électrodes des stimulateurs cardiaques.
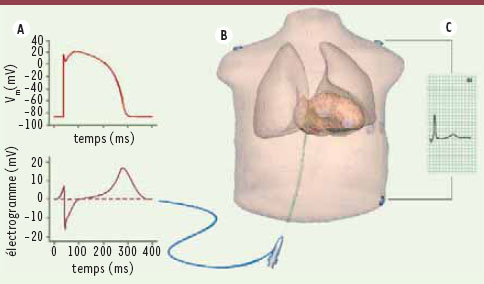
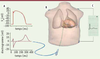 | Figure 5.
Insertion du cœur dans un modèle de torse A. Potentiel membranaire (haut) et électrogramme (bas) mesurable par un cathéter endocardique. B. Modèle du torse avec un cathéter endocardique et des électrodes thoraciques. C. Reconstruction de la dérivation III d’un ECG standard. |
|
On reconnaît de plus en plus que les mathématiques et la modélisation exercent un rôle important dans l’intégration des données sur le vivant qui se multiplient à diverses échelles [
28]. Traditionnellement, les modèles ont été utilisés pour vérifier et émettre des hypothèses sur les mécanismes fondamentaux régissant l’activité normale et pathologique du cœur. Les modèles se voulaient génériques puisqu’ils ne cherchaient pas à reproduire le détail de cas spécifiques. Une nouvelle tendance émerge actuellement qui veut aussi adapter les modèles aux caractéristiques de chaque patient de manière à contribuer au développement d’une médecine personnalisée [
29]. |
Les auteurs déclarent n’avoir aucun conflit d’intérêts concernant les données publiées dans cet article.M
|
Footnotes |
1. Rudy Y. From genetics to cellular function using computational biology. Ann NY Acad Sci 2004; 1015 : 261–70. 2. Hunter PJ, Borg TK. Integration from proteins to organs: the Physiome Project. Nat Rev Mol Cell Biol 2003; 4 : 237–43. 3. Brook BS, Waters SL. Mathematical challenges in integrative physiology. J Math Biol 2008; 56 : 893–6. 4. Restrepo JG, Weiss JN, Karma A. Calsequestrin-mediated mechanism for cellular calcium alternans. Biophys J 2008; 95 : 3767–89. 5. Saucerman J, Zhang J, Martin JC, et al. System analysis of PKA-mediated phosphorylation gradients in live cardiac myocytes. Proc Natl Acad Sci USA 2006; 103 :12923–8. 6. Austin TM, Hooks DA, Hunter PJ, et al. Modeling cardiac electrical activity at the cell and tissue levels. Ann NY Acad Sci 2006; 1080 : 334–47. 7. Moe GK, Rheinbolt WC, Abildskov JA. A computer model of atrial fibrillation. Am Heart J 1964; 67 : 200–20. 8. Xie F, Qu Z, Garfinkel A, Weiss JN. Electrical refractory period restitution and spiral wave reentry in simulated cardiac tissue. Am J Physiol Heart Circ Physiol 2002; 283 : H448–60. 9. Comtois P, Sakabe M, Vigmond EJ, et al. Mechanisms of atrial fibrillation termination by rapidly unbinding Na+ channel blockers: insights from mathematical models and experimental correlates. Am J Physiol 2008; 295 : H1489–504. 10. Kléber AG, Rudy Y. Basic mechanisms of cardiac impulse propagation and associated arrhythmias. Physiol Rev 2004; 84 : 431–88. 11. Lim ZY, Maskara B, Aguel F, et al. Spiral wave attachment to millimeter-sized obstacles. Circulation 2006; 114 : 2113–21. 12. Ikeda T, Yashima M, Uchida T, et al. Attachment of meandering reentrant wave fronts to anatomic obstacles in the atrium. Role of obstacle size. Circ Res 1997; 81 : 753–64. 13. Li D, Fareh S, Leung TK, et al. Promotion of atrial fibrillation by heart failure in dogs: atrial remodelling of a different sort. Circulation 1999; 100 : 87–95. 14. Hanna N, Cardin S, Leung TK, et al. Differences in atrial versus ventricular remodelling in dogs with ventricular tachypacing-induced congestive heart failure. Cardiovasc Res 2004; 63 : 236–44. 15. Pastore JM, Rosenbaum DS. Role of structural barriers in the mechanism of alternans-induced reentry. Circ Res 2000; 87 : 1157–63. 16. Comtois P, Vinet A. Curvature effects on activation speed and repolarization in an ionic model of cardiac myocytes. Phys Rev E 1999; 60 : 4619–28. 17. Sampson KJ, Henriquez CS. Interplay of ionic and structural heterogeneity on functional action potential duration gradients: Implications for arrhythmogenesis. Chaos 2002; 12 : 819–28. 18. Ten Tusscher KHWJ, Panfilov AV. Influence of non excitable cells on spiral breakup in two-dimensional and three-dimensional excitable media. Phys Rev E 2003; 68 : 062902. 19. Ten Tusscher KHWJ, Panfilov AV. Wave propagation in excitable media with randomly distributed obstacles. Multiscale Modeling Simulation 2005; 3 : 265–82. 20. Malik M, Camm AJ. Components of heart rate variability- what they mean and what we really measure. Am J Cardiol 1993; 72 : 821–22. 21. Ghosh S, Rhee EK, Avari JN, et al. Cardiac memory in patients with Wolff-Parkinson-White syndrome; noninvasive imaging of activation and repolarization before and after catheter ablation. Circulation 2008; 118 : 907–15. 22. Potse M, Coronel R, Leblanc AR, Vinet A. The role of extracellular potassium transport in computer models of the ischaemic zone. Med Biol Eng Comput 2007; 45 : 1187–99. 23. Henriquez CS. Simulating the electrical behavior of cardiac tissue using the bidomain model. CRC Crit Rev Biomed Eng 1993; 21 : 1–77. 24. Plank G, Zhou L, Greenstein JL, et al. From mitochondrial ion channels to arrhythmias in the heart: Computational techniques to bridge the spatio-temporal scales. Philos Transact A Math Phys Eng Sci 2008; 366 : 3381–409. 25. Potse M, Dubé B, Richer J, et al. A comparison of monodomain and bidomain reaction-diffusion models for action potential propagation in the human heart. IEEE Trans Biomed Eng 2006; 53 : 2425–35. 26. Potse M, Baroudi G, Lanfranchi PA, et al. Generation of the T wave in the electrocardiogram: lessons to be learned from long-QT syndromes. Can J Cardiol 2007; 23 : 238C. 27. Miller WT, Geselowitz DB. Simulation studies of the electrocardiogram; I. The normal heart. Circ Res 1978; 43 : 301–15. 28. Sideman S. The challenge of cardiac modeling-interaction and integration. Ann NY Acad Sci 2006; 1080 : XI-XXIII. 29. Reumann R, Gurev N, Rice JJ. Computational modeling of cardiac disease: potential for personalized medicine. Personnalized Med 2009 : 45–66. 30. Vinet A, Chialvo DR, Michaels DC, Jalife J. Nonlinear dynamics of rate-dependent activation in models of single cardiac cells. Circ Res 1990; 67 : 1510–24. |