Les mitochondries (Figure 1) sont des organites cellulaires entourés de deux membranes qui sont considérées comme la centrale énergétique de la cellule [ 1– 3] (→). L’énergie produite par les mitochondries sous forme d’ATP provient de la réaction de l’oxygène avec les produits de dégradation de notre alimentation qui sont essentiellement réducteurs (Figure 2). Les produits ultimes de cette dégradation entraînent la conversion des coenzymes oxydés NAD⁺ et FAD (flavine adénine dinucléotide) en leurs équivalents réduits NADH et FADH ₂. La rencontre des coenzymes réduits, véritables monnaies d’échange des réactions d’oxydoréduction, avec l’oxygène ne se fait pas directement mais à travers une série de réactions d’oxydoréduction successives catalysées par des complexes protéiques hautement structurés, numérotés de I à IV (Figure 3). C’est au niveau des complexes I, III et IV que s’opère la récupération de l’énergie sous la forme d’un gradient de protons H⁺ extraits de l’intérieur des mitochondries vers l’espace intermembranaire. Ce gradient électrochimique de protons permet ensuite la synthèse d’ATP à travers un autre complexe protéique, l’ATP synthase (appelé aussi quelquefois complexe V), qui est un véritable moteur moléculaire [ 4]. 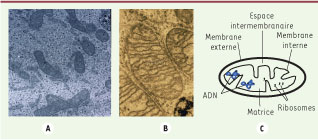C’est la théorie chimio-osmotique de Mitchell [ 5, 6].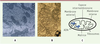

Figure 1 Images de mitochondries en microscopie électronique et schéma classique de l’organisation des mitochondries. A. Mitochondries de fibroblastes de peau, microscope électronique à transmission (source : Vincent Procaccio, © Inserm, Serimedis). B. Image en microscopie électronique de trois mitochondries à l’intérieur d’une cellule du foie en culture (source : Bruno Clément, © Inserm, Serimedis). C. Schéma d’une mitochondrie.

Figure 1 Images de mitochondries en microscopie électronique et schéma classique de l’organisation des mitochondries. A. Mitochondries de fibroblastes de peau, microscope électronique à transmission (source : Vincent Procaccio, © Inserm, Serimedis). B. Image en microscopie électronique de trois mitochondries à l’intérieur d’une cellule du foie en culture (source : Bruno Clément, © Inserm, Serimedis). C. Schéma d’une mitochondrie.

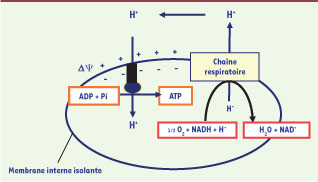
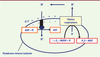Figure 2 La théorie chimio-osmotique de Mitchell. Le couplage entre les réactions d’oxydoréduction de la chaîne respiratoire et la synthèse d’ATP se fait par l’intermédiaire d’un gradient de protons induisant à la fois une différence de concentration en protons [Hex +] > [Hin +] et une différence de potentiel Δѱ.

Figure 2 La théorie chimio-osmotique de Mitchell. Le couplage entre les réactions d’oxydoréduction de la chaîne respiratoire et la synthèse d’ATP se fait par l’intermédiaire d’un gradient de protons induisant à la fois une différence de concentration en protons [Hex +] > [Hin +] et une différence de potentiel Δѱ.

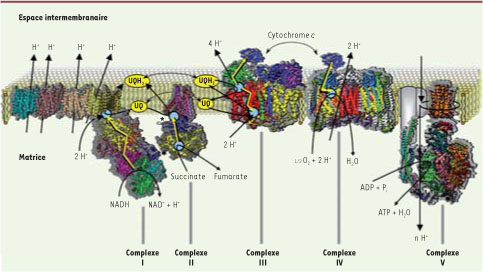
Figure 3 Les oxydations phosphorylantes mitochondriales. Les transferts d’électrons au sein des complexes sont représentés par des flèches jaunes. Les sites de couplage explicite entre transfert d’électrons et de protons sont indiqués par des cercles bleus clairs. Les sites de couplage au niveau du complexe II sont signalés par des astérisques; le transfert de protons n’a pas été indiqué ici car les deux réactions se neutralisent (l’oxydation du succinate libère deux protons et la réduction de l’ubiquinone [UQ] les reprend). Les protons transportés par un mécanisme de pompe (complexes I et IV) sont indiqués par des flèches noires traversant les complexes. Les stœchiométries indiquées sont pour deux électrons (donc une molécule de NADH ou une demi-molécule d’oxygène) (© figure et légende réalisées par Francis Haraux).

Figure 3 Les oxydations phosphorylantes mitochondriales. Les transferts d’électrons au sein des complexes sont représentés par des flèches jaunes. Les sites de couplage explicite entre transfert d’électrons et de protons sont indiqués par des cercles bleus clairs. Les sites de couplage au niveau du complexe II sont signalés par des astérisques; le transfert de protons n’a pas été indiqué ici car les deux réactions se neutralisent (l’oxydation du succinate libère deux protons et la réduction de l’ubiquinone [UQ] les reprend). Les protons transportés par un mécanisme de pompe (complexes I et IV) sont indiqués par des flèches noires traversant les complexes. Les stœchiométries indiquées sont pour deux électrons (donc une molécule de NADH ou une demi-molécule d’oxygène) (© figure et légende réalisées par Francis Haraux).

(→) Voir les trois articles de la série Dynamique mitochondriale publies dans le numéro d’octobre 2010 de Médecine/Sciences, pages 823-841

La structure de la plupart des complexes de la chaîne respiratoire est maintenant connue (Figure 3). Les structures cristallines permettent de prédire assez clairement un cheminement des électrons et, dans certains cas, des protons associés à la réaction d’oxydoréduction catalysée par ces complexes. Dans le cas du complexe III (ou complexe bc ₁), deux chemins pour les électrons furent mis en évidence (Figure 4) lors de l’établissement de la structure cristallographique. Cette découverte venait conforter une hypothèse faite également par Mitchell en 1975 [6, 7] sous le nom de « cycle Q » ou « cycle des quinones » dans lequel il était postulé, et c’était l’hypothèse de base, que les deux électrons apportés par la molécule de quinol (QH₂) suivaient des chemins différents (Figure 5).

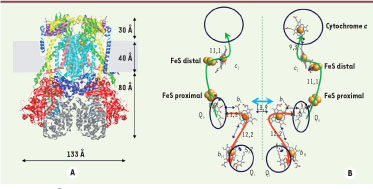
Figure 4 Structure du complexe bc1 dimérique. A. Structure du cristal de complexe bc 1 de bœuf (PDB [protein data bank] Id : 2A06). La position de la membrane est figurée en gris. B. Vue des différents groupes prosthétiques et des sites de fixation des quinones (entourés) dans le cytochrome bc 1 (dimère). Le site de fixation du cytochrome c est aussi entouré. Les distances bord a bord entre les différents centres sont données en Å. On notera les deux positions possibles, proximale et distale, du centre FeS associées au mouvement de la tête de la protéine nommée protéine de Rieske. On notera aussi la distance de 13,9 Å entre les hèmes bL permettant un échange d’électrons entre les deux monomères du dimère. Les sites QO et Qi sont occupés par une molécule de quinone. Les deux chemins possibles des électrons sont figurés en orange et vert.

Figure 4 Structure du complexe bc1 dimérique. A. Structure du cristal de complexe bc 1 de bœuf (PDB [protein data bank] Id : 2A06). La position de la membrane est figurée en gris. B. Vue des différents groupes prosthétiques et des sites de fixation des quinones (entourés) dans le cytochrome bc 1 (dimère). Le site de fixation du cytochrome c est aussi entouré. Les distances bord a bord entre les différents centres sont données en Å. On notera les deux positions possibles, proximale et distale, du centre FeS associées au mouvement de la tête de la protéine nommée protéine de Rieske. On notera aussi la distance de 13,9 Å entre les hèmes bL permettant un échange d’électrons entre les deux monomères du dimère. Les sites QO et Qi sont occupés par une molécule de quinone. Les deux chemins possibles des électrons sont figurés en orange et vert.

Figure 5 Le cycle Q de Mitchell. A. Le schéma original de Mitchell [7]. B. Schéma actuel prenant en compte la structure connue d’un monomère de cytochrome bc 1. On notera les deux sites Qo et Qi de fixation des quinones et les deux chemins d’électrons : l’un par FeS vers le haut de la figure, l’autre par b L, b H et Qi vers le bas. En comparant avec le schéma de Mitchell, c correspond à FeS et les deux centres d et bR correspondent maintenant au seul centre bH intervenant deux fois successivement.

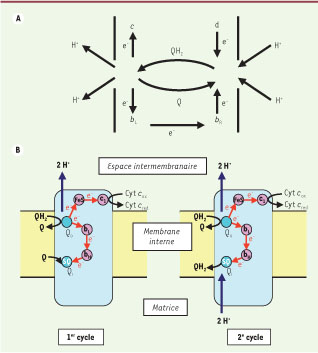
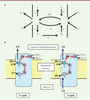Figure 5 Le cycle Q de Mitchell. A. Le schéma original de Mitchell [7]. B. Schéma actuel prenant en compte la structure connue d’un monomère de cytochrome bc 1. On notera les deux sites Qo et Qi de fixation des quinones et les deux chemins d’électrons : l’un par FeS vers le haut de la figure, l’autre par b L, b H et Qi vers le bas. En comparant avec le schéma de Mitchell, c correspond à FeS et les deux centres d et bR correspondent maintenant au seul centre bH intervenant deux fois successivement.

Nous décrirons dans cet article comment une approche stochastique prenant en compte la structure maintenant connue du complexe III et les potentiels redox standard des différents centres redox permet de montrer que le complexe III fonctionne réellement selon l’hypothèse du « cycle Q » de Mitchell.

Comme on le voit sur la Figure 3, le complexe III est central dans la chaîne respiratoire. Il est en effet situé entre d’une part, les complexes I, II et diverses déshydrogénases qui réduisent l’ubiquinone (Q) en ubiquinol (QH₂) et d’autre part, la cytochrome oxydase ou complexe IV qui catalyse l’oxydation par l’oxygène du cytochrome c réduit en cytochrome c oxydé. Globalement la réaction catalysée par le complexe III peut s’écrire :

QH₂ + 2 cyt c _ox ==> Q + 2 cyt c _red + 2 H⁺ (1)

Pour expliquer les propriétés cinétiques et thermodynamiques particulières du complexe III et l’apparente absence de transporteur de protons, Mitchell, en 1975 [6, 7], fait l’hypothèse de l’existence de deux sites de fixation des quinones sur le complexe III, dont l’un, Q_o, près de la face externe de la membrane mitochondriale interne, fixera préférentiellement QH₂ et libérera 2 H⁺ a l’extérieur, et l’autre, Q_i, près de la face interne de la membrane mitochondriale interne, fixera préférentiellement Q et captera 2 H⁺ pour former QH₂. Tout se passerait comme si les quinones jouaient le rôle de transporteurs de H⁺. Les électrons d’une molécule de QH₂ fixée en Q_o pourront quant a eux emprunter deux chemins : l’un vers la réduction du cytochrome c, l’autre a l’intérieur du complexe III pour aller réduire la molécule de Q. Comme il faut deux électrons pour cela, il faudra deux cycles qui peuvent s’écrire de la manière suivante :

Q⁻ désigne la molécule de semiquinone qui sera notée SQ dans la suite. Q_oH₂ indique une molécule de QH₂ fixée en Q_o, Q_i, une molécule de Q₀ fixée en Q_i, etc.

Ce très subtil schéma de fonctionnement proposé par Mitchell a servi d’hypothèse de travail jusqu’à maintenant. Il a permis d’interpréter l’ensemble des données expérimentales et il existe un consensus très général pour accepter ce mécanisme.

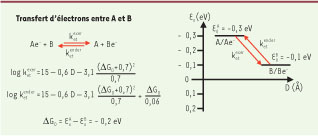
Toutefois depuis 1998, la structure cristallographique du cytochrome bc ₁ est connue avec une bonne précision [ 8, 9] (Figure 4A). Cette structure a effectivement révélé deux sites de fixation pour les quinones/quinols ainsi que deux chemins possibles pour les électrons à partir du site Q_o (Figure 4B). Par ailleurs, les travaux de Leslie Dutton et Chris Moser [ 10] ont permis de déterminer de manière générale les constantes de vitesse théoriques des réactions d’oxydoréduction par effet tunnel, en fonction principalement de la distance entre les centres réactionnels et de la différence de potentiel d’oxydoréduction standard entre les centres réactionnels (Figure 6). Les distances entre les centres réactionnels sont maintenant connues grâce à la cristallographie et les potentiels d’oxydoréduction standard ont été mesurés depuis longtemps. Nous avons donc en principe tous les éléments pour calculer les constantes de vitesse de réaction entre les centres d’oxydoréduction et ainsi simuler son fonctionnement.

Figure 6 Formules deMoseret Dutton. Les formules [10] donnent les constantes de vitesse ke exer et ket ender pour le transfert d’un électron entre deux couples redox A/Ae− et B/Be−. ket exer désigne la constante de vitesse de la réaction dans le sens le plus favorable (exergonique, de A vers B dans notre exemple) et ket ender dans le sens inverse (endergonique, l’électron doit « monter » de B vers A). D est la distance, bord a bord, entre les centres redox A et B (hèmes, FeS, sites de fixation).

Figure 6 Formules deMoseret Dutton. Les formules [10] donnent les constantes de vitesse ke exer et ket ender pour le transfert d’un électron entre deux couples redox A/Ae− et B/Be−. ket exer désigne la constante de vitesse de la réaction dans le sens le plus favorable (exergonique, de A vers B dans notre exemple) et ket ender dans le sens inverse (endergonique, l’électron doit « monter » de B vers A). D est la distance, bord a bord, entre les centres redox A et B (hèmes, FeS, sites de fixation).

Les réactions d’oxydoréduction à l’intérieur d’une molécule de cytochrome bc ₁ sont des événements isolés. Une modélisation classique par équations différentielles est donc mal adaptée dans ce cas, car ces dernières, par principe, traitent de réactions entre des populations de molécules. Nous devons plutôt considérer ici une seule macromolécule de complexe bc ₁ avec des passages aléatoires d’un électron entre les centres redox. Cette approche stochastique des réactions chimiques ou enzymatiques a été abordée par Gillespie [ 11]. La méthode est relativement simple. La probabilité d’occurrence d’une réaction i est proportionnelle à la valeur de a_i = k_i x |A_i| (on considère ici seulement des réactions simples du type A => B ou transfert d’un électron; |A_i| désigne le nombre de molécules de l’espèce A_i; et k_i la constante de vitesse de la réaction i. Autrement dit, une réaction a d’autant plus de chance de survenir qu’elle est rapide.

Il suffit donc d’effectuer un tirage au sort pour choisir la première réaction i qui aura lieu à un instant donné. Pour ce faire, on construit un intervalle (ou segment) de longueur a₀=Σa_i en mettant bout à bout dans un ordre quelconque les différents intervalles a_i. Puis on tire au sort un nombre r_i compris entre 0 et a₀. Le segment i à l’intérieur duquel tombe ce nombre donne la réaction qui aura lieu. Il faut ensuite déterminer le temps auquel elle aura lieu. Pour cela, on se base sur le fait que cette réaction i se produira avec une probabilité donnée par une loi exponentielle dont la constante est a_o (et non a_i), ce qui amène à tirer un deuxième nombre au hasard u₁ entre 0 et 1. Le temps τ₁ = −1/a₀. ln(uj) auquel cette réaction aura lieu est ajouté au temps initial (t = 0 en général), les nouveaux états oxydés/réduits, c’est-à-dire 0 ou 1 électron, sont recalculés et le processus est recommencé avec le choix de la nouvelle réaction qui prendra place (tirage de r₂) et la détermination du temps τ₂ (tirage de u₂) au bout duquel elle aura lieu après la première réaction (t = τ₁ + τ₂, etc.) (voir deux exemples simples en matériels supplémentaires¹).

On a appliqué l’approche de Gillespie à la simulation du fonctionnement d’une molécule unique de complexe bc ₁. Rappelons que les électrons, une fois engagés à l’intérieur d’une molécule de complexe bc ₁, ne passent pas sur une autre molécule de complexe bc ₁. Le modèle comporte 20 réactions par monomère, ce qui fait 78 réactions par dimère en tenant compte de la réversibilité et du fait qu’une des réactions traduit le passage des électrons entre les monomères à travers les hèmes b_L (elle ne doit pas être comptée deux fois). La Figure 7 montre le résultat de 30 simulations stochastiques comportant plus de 12 000 000 réactions chacune. On a suivi la réduction des molécules de cytochrome c, produit final de la réaction, dans un état stationnaire comprenant la réoxydation continue de cytochrome c et la réduction continue de Q en QH₂, ces deux étapes n’étant pas considérées comme limitantes. 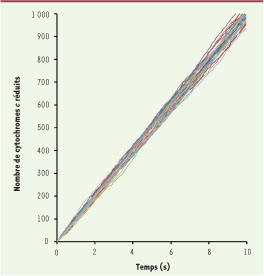On obtient une vitesse de réaction d’environ 100 s⁻¹ qui est de l’ordre de ce qui est observé expérimentalement [ 12– 14].

Figure 7 Cinétique globale de réduction du cytochrome c en fonction du temps par une molécule de cytochrome bc 1 . La igure représente le résultat de 30 simulations faisant intervenir plus de 12 000 000 pas de programme (deux tirages au hasard chaque fois : choix de la réaction et temps au bout duquel se fait la réaction choisie). Les molécules de Q produites sont rapidement réduites et le cytochrome c réduit rapidement oxydé pour assurer, de manière non limitante, un état stationnaire. La vitesse dans ces conditions est de l’ordre de 100 s−1.

Figure 7 Cinétique globale de réduction du cytochrome c en fonction du temps par une molécule de cytochrome bc 1 . La igure représente le résultat de 30 simulations faisant intervenir plus de 12 000 000 pas de programme (deux tirages au hasard chaque fois : choix de la réaction et temps au bout duquel se fait la réaction choisie). Les molécules de Q produites sont rapidement réduites et le cytochrome c réduit rapidement oxydé pour assurer, de manière non limitante, un état stationnaire. La vitesse dans ces conditions est de l’ordre de 100 s−1.

Ce résultat, toutefois, ne nous renseigne pas sur la manière dont s’effectue le passage des électrons dans le complexe bc ₁. En particulier, on ne sait pas si l’on a affaire à un mécanisme obéissant au schéma du cycle Q de Mitchell ou non. Le principe du cycle Q de Mitchell est la séparation des deux électrons issus de QH₂ en Q_o, l’un partant vers FeS², c ₁ et c, l’autre vers b_L, b_H et Q_i (Figure 4). De nombreux résultats expérimentaux indiquent que les deux électrons bifurquent pratiquement en même temps de manière dite concertée et de nombreux mécanismes ont été imaginés pour assurer cette concertation (plutôt qu’un passage des deux électrons à la suite vers le cytochrome c). Qu’en est-il dans nos simulations, en absence de toute hypothèse additionnelle ? Le résultat est donné dans la Figure 8 où l’on a représenté pour chaque nouvelle molécule QH₂ fixée le devenir des électrons libérés en Q_o, soit vers FeS (puis réduction du cytochrome c ₁ puis c) soit vers l’hème b _L puis b _H et Q_i. Cette figure, qui illustre le passage cumulé des électrons correspondant a la fixation successive de 1 000 molécules de quinol (QH₂), montre que pratiquement autant d’électrons passent normalement vers FeS, c ₁ et c que vers b _L puis b _H et Q_i. Au début même les deux courbes sont confondues, indiquant une bifurcation parfaite, puis on voit apparaître un très petit nombre d’électrons qui passent vers FeS (pour réduire c ₁) plutôt que d’aller vers b _L. C’est ce qui est désigné sous le terme de « courtcircuit », c’est-à-dire un circuit d’électrons ne prenant pas de protons à l’intérieur de la mitochondrie.

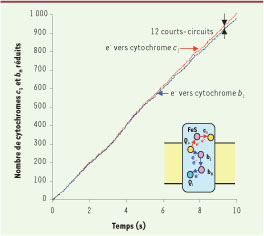
Figure 8 La bifurcation des électrons en Q o . Le nombre d’électrons passant vers le cytochrome c 1 et de ceux passant vers le cytochrome b L ont été représentés. La figure montre clairement que ce nombre est pratiquement identique, indiquant une séparation quasi systématique des deux électrons du QH2 dans chacune des deux voies.

Figure 8 La bifurcation des électrons en Q o . Le nombre d’électrons passant vers le cytochrome c 1 et de ceux passant vers le cytochrome b L ont été représentés. La figure montre clairement que ce nombre est pratiquement identique, indiquant une séparation quasi systématique des deux électrons du QH2 dans chacune des deux voies.

On peut donc dire que la structure des centres redox au sein du complexe bc ₁ (en particulier les distances entre les centres) et les potentiels de demi-réduction de ces centres redox sont tels qu’ils conduisent automatiquement, dans pratiquement tous les cas, au mécanisme du cycle Q imaginé par Mitchell. Il n’est pas nécessaire d’invoquer une hypothèse supplémentaire. On peut montrer [ 15] que le « premier électron » d’une molécule de QH₂ passe par la voie FeS-c ₁-c alors que le « deuxième » emprunte la voie b _L-b _H-Q_i. Cela est dû au fait que le premier électron de QH₂, en passant sur FeS, dévoile un deuxième électron associé a un potentiel standard beaucoup plus bas (couple SQ/Q) qui lui permet d’aller sur b_L (pas sur FeS occupé) alors que le premier ne le pouvait pas d’un point de vue thermodynamique (potentiel standard du couple QH₂/SQ plus élevé). Rappelons que les électrons étant chargés négativement, leur mouvement naturel, favorable, est du potentiel le plus bas au potentiel le plus haut.

Nous avons montré que le cycle Q de Mitchell est basé sur une forte séparation des potentiels redox standard associés au départ des deux électrons du quinol QH₂ [15]. Si la séparation est moins forte, on montre qu’il est alors possible que les deux électrons passent directement sur FeS vers le cytochrome c ₁. Cela assure le passage des électrons et donc la réduction du cytochrome c, ce qui est une des fonctions du complexe bc₁, mais cela diminue la différence de potentiel créée par le prélèvement des deux protons internes, ce qui est l’autre fonction assurée par le complexe bc ₁ (contribution à la force protomotrice pour la synthèse d’ATP). Les distances entre les centres ont aussi leur importance, en particulier, comme nous l’avons montré dans [ 16], entre Q_o et FeS, ce qui semble normal. Un peu pour les mêmes raisons, la distance entre Q_o et b _L est importante : si elle augmente trop, le passage du deuxième électron sur b _L ne sera plus aussi rapide et la semiquinone va résider plus longtemps sur Q_o augmentant la probabilité que le deuxième électron passe sur FeS plutôt que sur b _L. Pour les mêmes raisons, on montre que si la distance b _L-b _H augmente, le deuxième électron peut résider suffisamment longtemps sur b _L pour pouvoir réduire la semiquinone résultant de la fixation en Q_o d’une deuxième molécule de QH₂, établissant ainsi un court-circuit. Cela conduit à un déficit de potentiel membranaire et l’énergie qui n’a pas été utilisée pour prendre deux protons dans la matrice mitochondriale est nécessairement dissipée en chaleur (ou partiellement en production de radicaux libres). C’est ce qui peut arriver dans des mutants du complexe bc ₁ en pathologie humaine. Mais une telle production de chaleur peut présenter un avantage pour des populations dans des environnements nordiques. C’est ainsi que l’on explique l’adaptation au froid de certains individus ou de certaines populations. Nous avons montré par exemple que la diminution de l’affinité de Q en Q_i comme cela est suspecté dans certaines sous-classes de l’haplogroupe mitochondrial J ne change pas l’activité du complexe (k_cat inchangé) mais conduit à une légère augmentation de court-circuit, et donc théoriquement à une production de chaleur modérée. On voit donc tout l’intérêt d’un tel modèle pour comprendre le fonctionnement fin de ce complexe, les raisons des déficits mitochondriaux ou bien les avantages adaptatifs de certains haplogroupes (voir une discussion de ce problème des haplogroupes dans [ 17]). Jusqu’à maintenant, les mutations du complexe III humain intervenant dans des pathologies n’ont été trouvées que dans trois de ses sous-unités dont la sous-unité mitochondriale (cytochrome b), les deux autres étant nucléaires [ 18]. Les mutations équivalentes aux mutations humaines ont été introduites et étudiées dans la levure [ 19]. Ces mutants dans la levure (et leurs suppresseurs) pourraient s’avérer être des outils précieux pour éclairer le mécanisme fin de bifurcation des électrons et de mouvement des protons.

Les haplogroupes de l’ADNmt, la plupart du temps considérés comme neutres, peuvent cependant avoir une influence [ 20, 21], montrant par là que le polymorphisme des haplogroupes n’est pas complètement neutre mais peut avoir un retentissement (faible) sur le fonctionnement des complexes respiratoires en association ou non avec des mutations pathologiques. L’étude des changements d’acides aminés intervenant dans les cytochromes b de divers haplogroupes peut s’avérer utile pour comprendre des mécanismes de fonctionnement de ce complexe.

Le principal avantage de cette méthode est de ne pas limiter a priori le nombre des états oxydés/réduits du complexe bc ₁. Toutes les possibilités sont envisagées. On regarde simplement ce qui se passe, quelles réactions ont lieu, quelles espèces réagissent entre elles et pourquoi. Le résultat important de ce travail est de montrer que le passage des électrons dans le complexe bc ₁ s’opère bien dans plus de 98 % des cas selon le schéma du cycle Q proposé par Mitchell, et cela sans hypothèse supplémentaire (de gating, de concertation, etc.). En particulier, la concertation apparente du passage des deux électrons dans chacune des voies est une conséquence de la répartition des différentes probabilités (c’est-à-dire des constantes de vitesse) de passage de ces électrons et non le résultat d’un quelconque mécanisme assurant cette concertation.

Cette approche stochastique décrit ce qui se passe exactement (en vrai) au niveau des molécules de complexe bc ₁ et des électrons. Il apparaît sur nos simulations que la plus grande partie des réactions est constituée d’allers-retours (entre Q_oH₂ et FeS, b _L - b _H et b _H – Q_i principalement). C’est l’une des difficultés de cette approche théorique (que l’on ne rencontre pas en utilisant des équations différentielles) : dans la mesure où toutes les réactions sont comptabilisées, cela augmente considérablement les temps de calcul.

On rencontre une deuxième difficulté, déja évoquée : la détermination des quantités exactes des molécules de substrats et produits effectives dans les réactions stochastiques de fixation ou de libération aux sites Q_o et Q_i et au site de fixation du cytochrome c. On connaît assez bien le nombre relatif de quinones, de cytochrome c et de complexe bc₁ mais le volume utile, en partie membranaire, dans lequel ils opèrent est plus difficile à évaluer. Malgré ces réserves, on peut dire que l’approche stochastique est particulièrement utile pour décrire le fonctionnement intime des complexes de la chaîne respiratoire. Actuellement, nous appliquons cette approche aux autres complexes de la chaîne respiratoire dans le but de mieux comprendre le rôle central joué par le complexe III et le pool des quinones [ 22, 23]. Un certain nombre de questions restent en effet posées : y a-t-il compétition entre les déshydrogénases pour le même pool de quinones/ quinols ou existe-t-il des pools différents de quinones/quinols ? Le transfert des électrons entre les différents complexes par le coenzyme Q et le cytochrome c s’effectue-t-il par une diffusion au hasard entre les complexes ou bien au sein d’une organisation des complexes de la chaîne respiratoire en supercomplexes ? Quelle est dans ce modèle l’influence du gradient électrochimique en proton qui existe lors du fonctionnement normal de la chaîne respiratoire mitochondriale ? Comment décrire stochastiquement les dysfonctionnements de la chaîne respiratoire et la génération des radicaux libres ? Ce sont des questions auxquelles nous essayons de répondre à l’aide de cette approche stochastique.

Les auteurs déclarent n’avoir aucun conflit d’intérêts concernant les données publiées dans cet article.

Ce travail a reçu le soutien financier de l’ACI IMPBio de l’ANR SysBio/ BBSRC 2007 et des ateliers épigénomique, génopole et Université d’Évry. Les auteurs tiennent à remercier Gaël Brasseur, Alain Dautant, Francis Haraux, Anne Lombès et Brigitte Meunier pour leurs critiques constructives. Francis Haraux a réalisé la figure 3 et sa légende.